Repair Log: HP 3314A, Part 1

At a recent swap-meet I came across an HP 3314A Programmable Function Generator that was described as non-operational but was physically in good shape.

In my opinion, HP cases make great project boxes (see here, here, and here), and this case looked like it would be an excellent case for a future, yet-to-be-defined project.

And so I made an offer based solely on the idea of scrapping the 3314A's electronics but keeping its case and internal chassis.  The offer was accepted, and the 3314A came home with me.

But after I had returned home, I had second thoughts about my plan to scrap the unit.  Why not try to fix it, if that were possible?

And thus this blog post, which describes my efforts to bring this HP 3314A back to life.

Initial Power-On Error:

The first problem I came across was at power-up -- the unit would cycle through its initial count-down following power-up, and then it would hang.  The count numbers displayed during the Power-up cycle would often also be screwed up.  And at the end of this cycle, sometimes the 3314A would hang with the LED numerical display being blank, and sometimes the display would show Error Codes E13 or E43.

Looking in the manual (section 3-1), Error Code E13 does not exist, and, although Error Code E43 exists, it is an HP-IB Error Code meaning "Invalid Data."  Given that the instrument was not in Remote mode (i.e. HP-IB mode), the display of this last error code could be meaningless and a result of some other error.

Note that immediately following power-up, the unit's 3-digit numerical display should show the following sequential count-down:

999

888

777

666

555

444

333

222

111

000

The video, below, demonstrates the Count-down problem:

You can see from the video that the displays are changing, so the 3314A is attempting this count-down, but the digits of the first counts are screwed up.

But before I go any further...

A quick note on my initial trouble-shooting:

The HP Service Manual (downloadable from the Keysight website: HP 3314A Manuals) recommends trouble-shooting using Signature Analysis.  Unfortunately, I was at my wife's place in Nevada City, CA, at the time of this initial trouble-shooting, and my Signature Analyzer was back at my house in Silicon Valley, CA.

(Plus, the SA unit has been sitting in a box, untested, for at least 20 years (another swap-meet find), and I had no idea if it worked, or not, as I've never had a need to use it!)

So, this initial phase of trouble-shooting was done with a 2-channel oscilloscope...

Probing the Front Panel Assembly:

Because segments of the LED seven-segment displays were either being incorrectly kept off or, alternately, incorrectly illuminated, it made sense to start my trouble-shooting at the Keyboard assembly where the seven-segment displays reside.

But I immediately encountered several issues.  The first issue is that the HP schematic has a number of errors.

The image, below, shows my corrections, in red.  You can see that U1's (74LS273) inputs were incorrectly assigned.  Also, the pin number of the LED displays are incorrect.

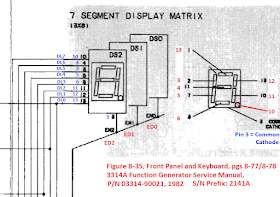
Here's a closeup of U1.  Its correct pin number assignments are shown in red:

And here's a closeup of the correct seven-segment display pinout (in red):

(Note that I also corrected the names of the three signals driving the common-cathode pins of these three displays to match the net names assigned to their respective drivers.)

The image below shows the correct pin number (in red) and the associated data bit from the 8-bit bus (in blue) for each segment of the LED.

When count-down sequence first starts, the first count presented on each seven-segment display is '9', and then this number counts down (8, 7, 6, etc.).  The numbers are the same on all three seven-segment displays, so the displayed numbers should be, in sequence, 999, 888, 777, 666, 555, etc.

Thus, the segments of the seven-segment display associated with data-bits DL0, DL1, DL2, and DL3 should be ON for the first count-down digits (9, 8, 7...), but, as you can see in the video, above, they are OFF.  These will later turn ON for lower counts (e.g. 3, 2, 1, 0), but at the start of count-down they are OFF.

The image below shows the problematic segments (highlighted in yellow):

The Keyboard assembly is a multiplexed system with the segments of the seven-segment displays sharing the same "row" signals (as in a row-column matrix) as the other front-panel LEDs.  Thus, probing a segment to see if it is correctly turning on or off can be a bit of a challenge with a two-channel scope, especially with the count-down's count quickly changing as it counts down.

But by observing U1's outputs (the 'LS273) responsible for driving the numerical segments immediately after power-on, it was clear that U1's outputs were not being set to the correct state to drive these segments ON for the first few counts (a U1 output bit must be set LOW to turn ON a segment).

Tracing this failure back...the data at U1's inputs, arriving at the Keyboard from the Controller Board,  was also in the incorrect state for these counts.  Thus, U1 was simply passing on incorrect data from the Controller Board.

So time to move the probing to the Controller Board...

Probing the Controller Board:

At the controller board I started at the processor, looking at its Data Bus while triggering the scope on the rising edge of the clock clocking data into the U1 register on the Keyboard assembly.  This probing showed that the data from the microprocessor that was being written to the Keyboard assembly was also incorrect.

So why was the processor writing incorrect data?  Was it getting bad data from the PROMs (of which there are six)?  Or was RAM bad?  Or was something fighting the bus when the processor was attempting to read or write this data?

Even though I did not have a Signature Analyzer, I decided to invoke one of its tests (SA Test #1, in which switches 1, 2, 7, and 8 are turned ON), because I assumed this test would sequentially count through all of the microprocessor's addresses and I could look for errors either on the Address Bus or on the Data Bus during this time.

Everything was looking good until I got to the CMOS SRAM, U211 and U212 (NEC UPD444/6514 1Kx4 bit CMOS RAM).  The four data I/O pins of U212 had flaky looking levels for some of its read cycles.  Plus, these flaky levels would change with time.  

The image below (lower scope trace) shows the levels one of these pins (pin 11, or I/O4).  U212's outputs are enabled whenever the upper trace is low.

Compared to U212, the I/O pins of U211 looked fine -- it was only U212's four data pins that had the issue.  And these four data bits correspond to the low-order four bits of the Data Bus, which were the problem bits driving the Keyboard's seven-segment displays.

Could a bad U212 be the culprit?  I placed an order of a pair of new NEC UPD444 RAMs on eBay, but while waiting for them to arrive I thought I'd continue testing...

By the way -- the HP manual has some errors regarding SRAM power on the Controller Board.  My corrections are shown, below, in red:

Excessive Battery Current Drain:

After ordering replacement UPD444 CMOS SRAM from eBay, I decided to look around a bit more and see what other problems I could find while waiting for the SRAM to arrive.

One issue I had noticed when I first opened up the unit was that the battery backup was dead (the battery was sitting at about 0.45 volts), yet it was a fairly new battery (with a 2023 date).  Could it have been killed by excessive current draw?

Note that this battery serves two purposes:

First, it keeps power applied to U203 of the RESET circuitry (CMOS inverters), even when power is OFF, so that the RESET line can be properly driven when power is first applied.

Second, the battery provides power to U211 and U212 (the CMOS SRAM), to maintain the contents in these two SRAM chips even when the unit is powered OFF.

Per section 5.2 of the manual, battery current drain when power was off should be on the order of 1.35 uA (typical) to 18.5 uA (max), when measured as an equivalent voltage drop across R13, a 1K ohm resistor -- e.g. 1.35 uA of current would equal 1.35 mV across R13).

Replacing the dead battery with a bench supply set to 3.0 volts, I measured 0.495 volts across R13 -- in other words, current draw was 495 uA, not the spec'd 18.5 uA max!

No wonder the battery was dead!

The battery-power circuit is fairly simple, which means there weren't many suspects.  And because U212 (one of the two CMOS SRAMS) was on my "hit-list" of suspected bad parts, I decided to clip its VCC pin (pin 18) and see what happened to battery current.  

With the pin clipped (i.e. no VCC applied to U212), the voltage across R13 dropped way down (below the level that my Fluke DVM can measure) -- clearly U212 was the culprit!  

U212 Temporary Replacement Test:

OK -- two different tests pointed to U212 being bad.  Was there some way that I could verify this while waiting for my eBay UPD444 CMOS RAM to arrive?

A friend gave me a National MM2114N-L 1Kx4 bit RAM from his junk box.  This device draws more supply current than the original NEC part, so it would not be a satisfactory permanent replacement for the UPD444, but I thought I would give it a try to test my theory that it was U212 that caused the count-down errors.

So I removed the original part, installed an 18-pin socket in its place, and inserted the '2114 in its place (also, the battery had been removed, too (it was dead) -- if the battery had been good, though, the MM2114N would have presented a much larger than expected current drain, and I would have removed it before doing this test).

I turned power on, and...nothing.  The seven-segment displays remained dark!

Probing with the scope, I quickly discovered that with power ON, Vcc at the '2114 was around 3 volts, not the expected 5 volts.  

Power to the CMOS RAM is a diode-OR'd combination of Vcc (via CR2, when the unit is powered up) or the Battery voltage (via CR3, when the unit is powered down and the CMOS RAM thus battery-powered).

There is a 49.9 ohm resistor (R17) in series with CR2.  The Vcc current of the '2114 RAM was enough to create a significant voltage drop across this 49.9 ohm resistor.

The obvious temporary solution was to short out the resistor for this test, which I did.

Powered the unit back ON, and the count-down was now correct!  Therefore, the count-down problem was caused by a bad U212 CMOS RAM IC.

Here's a video of the correct power-up countdown, with the MM2114N-L as the temporary replacement for U212:

Even thought the count-down is now correct, the unit still fails at the end of the count-down, either by blanking the seven-segment displays (as shown in the video, above) or showing (sometimes briefly) the two error codes mentioned above.

(An interesting question (unanswered) is why did HP add R17 in series with CR2?  My guess is that it has to do with current-limiting CR2's current at power-up, but why?  Note, its P/N is 1902-0535.  With 50 ohms in series and assuming a direct short from CR2's cathode to ground at power-up, CR2's initial current surge would be around 100 mA. Is the Schottky diode that sensitive to a temporary current surge?).

More Troubleshooting continues in Part 2!

Other Manual Issues:

Another Keyboard schematic error:  There are no net names assigned to the inputs of the four U5 drivers ('LS05 devices), so it is impossible to tell which output they actually connect to.

Resources:

HP 3314A Manuals:  https://www.keysight.com/us/en/support/3314A/programmable-function-generator.html

HP 3314A Repair in 3 parts:  https://diysquared.blogspot.com/2021/04/fixing-hp-3314a-function-generator-part.html

HP 3314A Repair on YouTube:  https://www.youtube.com/watch?v=wNxgBubSfH8

HP 3314A Repair (on Antique Radios forum):  https://antiqueradios.com/forums/viewtopic.php?f=8&t=360491

HP 3314A Teardown (EEVblog):  https://www.eevblog.com/forum/testgear/hp-3314a-function-generator-teardown-explanation/

HP 3314A Playing the Hallelujah Chorus:  https://www.youtube.com/watch?v=H90d6sPUF6A
(Note:  Hold down FUNCTION (the blue key), SW/TR INTVL, and START FREQ while powering up the unit).

HP 3314A ROM Images:  http://www.ko4bb.com/getsimple/index.php?id=manuals&dir=01_ROM_Images_and_Drivers/HP_3314A_Eprom

Standard Caveat:

As always, I might have made a mistake in my equations, assumptions, drawings, or interpretations.  If you see anything you believe to be in error or if anything is confusing, please feel free to contact me or comment below.

And so I should add -- this information is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE.

Representing a Transmission Line as a 2-Port Network

In this blog post I will derive equations representing a transmission line of characteristic impedance Zo and of length 'l' as a two-port network.  As a result, there will be a total of four different pairs of equations, each pair representing the two-port network in a different way.

These pairs of equation will be:

1.  V and I at Port 2, in terms of V and I at Port 1, for a lossy transmission line.

2.  V and I at Port 1, in terms of V and I at Port 2, for a lossy transmission line.

3.  V and I at Port 2, in terms of V and I at Port 1, for a lossless transmission line.

4. V and I at Port 1, in terms of V and I at Port 2, for a lossless transmission line.

(These last two sets of equations are special cases of the first two sets).

The image below shows these voltages and currents for both the transmission line and its two-port model.

The first two sets of equations that will be derived are summarized by the two matrix equations, below:

To derive the two equations in the first set of these equations, let's start with some fundamental definitions...

 

Some fundamentals:

Assume that the transmission line has on it both a forward voltage wave (traveling from left to right) and an independent reverse voltage wave (traveling from right to left).  At any point on the transmission line these forward and reverse voltage waves create forward and reverse current waves:

If we were to measure the voltage at any point on the line, the voltage we would measure at that point will be the sum of the forward voltage and the reverse voltage at that point.  

Note that the forward voltage and the reverse voltage each has its own amplitude and phase at that point.

Similarly, the current at that point will be the difference between the forward current and the reverse current (because the currents are flowing in opposite directions). 

Recognize that for either the forward wave or the reflected wave, their voltage and currents follow ohms law, independently of the other wave (because of the Principle of Superposition).  E.g. I⁺ = V⁺/Zo and I^-=V^-/Zo, where Zo is the transmission line's characteristic impedance.

So we can write equations for the Total Voltage and Current at each end of the transmission line in terms of the forward and reverse voltages at those points:

We can also express the forward and reverse voltages at either end of the transmission line as functions of the Total Voltage and Current at either end:

I will use equations 1, 2, 3, and 4 (in the figure, above) to derive the two-port network equations, but before I go any further in this derivation, let me first define a transmission line's "Propagation Constant."

Sidebar on the exponential terms e^-γl and e^γl :

Assuming a sinusoidal signal on the transmission line, the exponential term e^-γl  (or e^γl) represents the effect on a sine wave's amplitude and phase, due to the transmission line's Propagation Constant, γ, as that wave travels along the transmission line.

The other variable in the exponent is 'l', which represents the length that the wave has traveled (or will travel) along the transmission line.

The Propagation Constant is a complex number: γ = α + jβ, where α represents a "real" change in signal amplitude (either positive or negative, i.e. attenuation or gain), and jβ represents a phase shift of the sinusoidal signal, either a positive phase shift or a negative phase shift.  

Both of these values are in terms of unit-length, and so when substituted into the exponential, multiplying α by the length of the line gives overall attenuation (or gain, depending upon reference point), and multiplying jβ by length gives phase-shift for the wave's journey along a defined length of line.

If we were to take a snapshot in time and simultaneously compare the Forward Voltage V⁺ at point 1 with the Forward Voltage V⁺ at point 2, we would see that the voltage at point 2 has a negative phase shift compared to the phase of  V⁺ at point 1, because the voltage at point 2 represents an earlier version of  V⁺ that had been at point 1 at an earlier point in time, compared to the V⁺ that is currently at Point 1. 

We would also see that the amplitude of V⁺ at point 2 has been attenuated relative to its original amplitude at point 1 due to transmission line loss as it traveled from left to right along the line.   Thus, γ's "α" term (in the Propagation Constant's equation  γ = α + jβ) is negative to represent this loss at point 2 compared to the amplitude at point 1.

The figure below demonstrates both the attenuation and the phase shift at point 2, compared to point 1, for the Forward moving voltage wave:

With the same "snapshot in time," we can also simultaneously compare the Reverse Voltage V^- at point 1 with the Reverse Voltage V^- at point 2.  

We would see that the voltage at point 2 has a positive phase shift compared to the phase of  V^- at point 1, because the voltage at point 2 represents a later version of V^-  that has yet to arrive at point 1, compared to the phase of V^- that is currently at Point 1. 

We would also see that the amplitude of V^- at point 2 has not yet been attenuated compared to the amplitude of V^- at point 1, because it has not yet traveled from right-to-left along the line, and thus it has not yet been attenuated by line loss.  Therefore, γ's "α" term (in the Propagation Constant equation  γ = α + jβ) is positive for V^- at point 2 , not negative, because the amplitude at point 2 is larger compared to the amplitude at point 1.

The figure below demonstrates both the amplitude and phase at point 2, compared to point 1, for the Reverse moving voltage wave.:

With this information and the equations, above, we can derive network equations that represent a lossy transmission line of length 'l'.

Lossy Transmission Line Equations for V₂ and I₂ in terms of V₁ and I₁:

From the previous two figures that describe phase-shift and attenuation of V⁺ and V^- at Point 2 compared to our reference at Point 1, we can create the identities represented by equations 5 and 6 in the figure, below, and, using these, represent V₂ as a function of Point 1's V⁺ and V^- :

Similarly, we can represent the current I₂ at Point 2 as function of Point 1's V⁺ and V^- :

Next we substitute equations 1 and 2 (introduced earlier, above) into the V⁺ and V^- terms of these last two equations, rearrange, and get the following two equations:

Equations 9 and 10 represent V₂ and I₂ in terms of V₁ and I₁, and in themselves they satisfactorily represent the lossy transmission line as a two-port network (from the perspective of calculating V₂ and I₂ from V₁ and I₁).

But we can also represent these equations using Hyperbolic functions:

The matrix form of these last two equations is:

Lossy Transmission Line Equations for V₁ and I₁ in terms of V₂ and I₂:

In the same way that I defined V₂ and I₂ in terms of V₁ and I₁, I can define V₁ and I₁ in terms of V₂ and I₂.  (In fact, this is the typical form in which equations representing the transmission line as a two-port network appear).

This time, we begin by considering the Forward Voltage V⁺ and the Reverse Voltage V^-  from Point 2 (rather than from Point 1, as we did for the first derivations).

This will give us V⁺ and V^- at Point 1 in terms of  V⁺ and V^- at Point 2, as illustrated, below.

First, V⁺ at Point 1 in terms of  V⁺ at Point 2:  

Next, V^- at Point 1 in terms of  V^- at Point 2:

We can use these equations to represent the total Voltage at Port 1 in terms of V⁺ and V^- at Point 2:

Repeat for the total Current at Port 1:

Then, substituting into these two equations equations 3 and 4 (presented earlier) and rearrange.  We arrive at two equations expressing V₂ and I₂ in terms of V₁ and I₁:

The above form is a sufficient representation of these two equations, but often they will be represented in terms of Hyperbolic functions:

The matrix form of these last two equations is:

The above 2x2 matrix is in the form of an ABCD matrix (note that I2's direction is defined as exiting the network, not entering it).

Two-Port Network Equations for Lossless Lines:

Sometimes it is convenient to assume a transmission line is lossless.  What do I mean by lossless?

Recall the equation for the Propagation Constant: γ = α + jβ. If the line is lossless, α = 0 and thus e^-γl becomes e^-jβl. 

Similarly, e^γl becomes e^jβl. 

In either case, because α = 0, there is no attenuation as a wave travels along the transmission line, only phase shift.  With jβ and -jβ in the exponents of equations 9, 10, 17, and 18, we can use Euler's Formula and substitute cos and sin for the exponential terms in these four equations.

You can see equations 23 and 24 used in C. L. Ruthroff's article, "Some Broad-Band Transformers," in the August, 1959 issue of the "Proceedings of the I.R.E."

In matrix form, these equations are:

Note that these equations can also be expressed in terms of the Hyperbolic functions cosh and sinh in lieu of cos and sin.

Given γl = jβl, and using cos-cosh identities: cosh(γl) = cosh(jβl) = cos(j*jβl) = cos(-βl) = cos(βl).

The sinh term is similar:  sinh(γl) = sinh(jβl) = -j*sin(j*jβl) = -j*sin(-βl) = j*sin(βl).

Resources:

For further reading...

"Some Broad-band Transformers", C.L. Ruthroff, Proceedings of the IRE, August, 1959

"New Method of Impedance Matching in Radio-Frequency Circuits", G. Guanella, The Brown Boveri Review, September, 1944

"Transmission Line Transformers," Chapter Six of Radio Frequency Circuit Design, W. Alan Davis, Krishna Agarwal, John Wiley & Sonse, Inc. 2001

"A novel topology of Broad-band Coaxial impedance transformer", Centurelli, Piatella, Tommasino, Trifiletti, Proceedings of the 40th European Microwave Conference"

Phasors and Transmission Lines


And viewing...

Transmission Line YouTube Series, Professor Gregory D. Durgin, Georgia Tech.  Starting with this video:  https://www.youtube.com/watch?v=7Oz1sazpekM


Standard Caveat:

As always, I might have made a mistake in my equations, assumptions, drawings, or interpretations.  If you see anything you believe to be in error or if anything is confusing, please feel free to contact me or comment below.

And so I should add -- this information is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE.