Class E/F Exciter for the 813 AM Transmitter

This exciter replaces the Johnson Ranger that I'd originally used to drive my 813 AM Transmitter (described here, here, and here). It uses a modern Class E/F PA (described in further detail here), and it has a separate audio amplifier to drive the modulator deck in the 813 rig.

   

(Click on image to enlarge)

There is one major difference, however, between my original Class E/F PA, which was designed to generate 40 watts of RF power, and this final PA. This difference commences with a big...

   

Oops!

For when I connected this exciter to the 813 rig and keyed it for its initial "smoke test," the 813 Transmitter's grid-current meter pegged. 

Oops! 

But this shouldn't be! I'd measured the power output of the Ranger when it was driving the 813 Transmitter, and this output was around 40 watts for me to drive the 813 rig to about 350 watts. My exciter put out the same power. What was going on?  

As an experiment, I took a 50 ohm 6 dB high-power attenuator (that had been wired-in under my operating position) and connected it between the new exciter and the 813 PA's RF input. When I keyed the rig, the PA's grid current rose to about 22 mA -- right around where it was when the Ranger was driving the rig. 

Hmmm... 

I poked around and discovered that the 6 dB attenuator I'd just tested with had originally been installed between the Ranger and the 813 transmitter. I'd forgotten about it, and I'd assumed that the Ranger had been directly driving the 813 rig with 40 watts, when in reality it had been driving the 813 transmitter rig with one-quarter of this power! Doh. Dope slap!  

An obvious solution was to keep the 6 dB high-power pad connected between my exciter and the 813 PA Deck's input, but this seemed like a waste of a good attenuator (high-power attenuators are expensive, after all). Was there another, simpler, way to decrease the output power of my exciter by a factor of 4? 

A Slight Change to the Design... 

The Exciter's voltage for the FET Drains was 26 volts. If I halved this value, then, in principle, I ought to get a quarter of the power (power changes with the square of voltage). 

Luckily, the design already has a 12V switching regulator (rated to 3 Amps), so I just moved the connection for the FET Drain power from 26V to the output of the 12V switching regulator. Keyed it up, and, voila, it worked! The meter readings for the 813 were where they were when driven with the Ranger. 

Length Matters... 

One interesting phenomena that I noticed when doing this, though: during my initial testing, I'd connected the Exciter's RF output to the PA's RF input through two lengths of RG-58 coax (because I'd originally placed the 6 dB pad between these two lengths) for a combined length of about 9 feet. Later, when I shortened the total coax between the Exciter and the PA Deck from about 9 feet to 3 feet, the PA Deck's Grid Current started reading in the 35 mA range rather than in the original 20 mA range and the Exciter's Drain current jumped from about 0.8 A to 1.2A. Neither of these were desired changes, so I went back to my original 9 feet of coax to interconnect the Exciter to the PA Deck. 

Why does a change of 6 feet make such a difference in operation? At the moment, I don't know. However, as the length of the interconnecting coax is shortened, Exciter Drain current increases (from about 0.8A with 9 feet of coax to about 1.2A with 3 feet of coax), so the implication is that, with shorter coax, the Exciter is seeing a lower load resistance. This then implies that the PA Deck's RF input doesn't look like 50 ohms resistive, and thus there is an impedance transformation taking place via the 50 ohm coax. 

(I connected an HP 3577A network analyzer to the exciter-end of the coax feeding the PA Deck. With the PA grid tuning set to peak grid current (when the exciter was connected), I made the following measurements:

• 9' coax: S11 mag: 0.92, S11 angle: -13.2
• 4.5' coax: S11 mag: 0.67, S11 angle: -24.1

When converted into a parallel representation of real and imaginary impedance components (because, after all, the Exciter's tank consists of parallel-connected components, not series), the resulting values are:

• 9' coax: Real: 47.4 Ω, Imaginary: -j202 Ω
• 4.5'coax: Real: 36.8 Ω, Imaginary: -j82 Ω

Assuming that the Exciter tank is tuned to compensate for the imaginary component, the Exciter tank sees a lower resistive component with shorter coax, which correlates with the increased Drain current that I see, and the resistive component with 9' of coax is quite close to 50 ohms. 

However, there is one puzzle that I don't yet understand: with 4.5' of coax, the imaginary component represents more parallel capacitance than that of the 9' coax, yet I find that, when tuning the Exciter's tank when using the 4.5' length of coax, I need to turn the Exciter's Tank capacitor to full-mesh (i.e. high-capacitance) for best-looking Exciter RF. Why do I need to add more exciter-tank capacitance when I've already added more capacitance at the exciter load? It doesn't make sense to me. Should I be working with the series-form of impedance instead (in which the impedance measured at the end of the 4.5' length of coax has less capacitance than the 9' length)? Have I made a mistake in my measurements? I don't know. 

Well, something to research on another day... 

Other notes: 

Note 1: If I'd kept the 6 dB attenuator connected between the Exciter and the PA Deck, then the effect of coax-length on Exciter performance would be less of an issue, because the attenuator would have "buffered" the effect of the PA Deck's input impedance on the Exciter. 

Note 2: There is interaction between the Exciter's Tuning capacitor and the PA Deck's Grid Tuning capacitor; the position of one will affect the other. That is, the amount of "junk" on the Exciter's RF waveform (monitored at the front-panel BNC) will change, depending upon how the Grid Tuning capacitor is changed. When tuning the transmitter:

1. First I peak the PA Deck's Grid current.
2. Then I adjust the Exciter Tank tuning for best looking RF at the Exciter's output (as observed at the Exciter's front-panel BNC). This is typically at, or near, minimum Drain current, as measured on the Exciter's front-panel meter.

Here's a screen-shot of bad-looking RF from the Exciter. Its tank needs tuning!

   

(Click on image to enlarge)

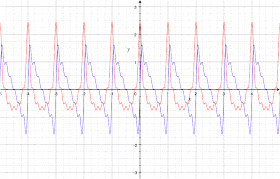
And here's the Exciter RF with its tank properly adjusted:

   

(Click on image to enlarge)

(Exciter RF waveform measured at the front-panel BNC, J6, using a Tektronix TDS320 scope (100 MHz bandwidth).) Schematics. There are four pages. Here they are:

   

(Page 1. Click on image to enlarge)

Notes on page 1: This page is essentially the same as the original design, but changes are:

• DC Voltage for IRF530s changed from 26 VDC to 12 VDC.
• 510 pf added to tank circuit (3570 pf total) so that the Tank circuit, when operating at 3.87 MHz, is properly tuned with Tuning Capacitor C11 at about half-mesh.

(Page 2. Click on image to enlarge)

Notes on page 2: 

No change from the original circuit. But because the LM2576 switching-regulator now must deliver an additional 800 mA (or so, to power the PA FETs), the inductor L3 really should be changed from 1000 uH to 470 uH or 330 uH. But it seems to run fine with the original value of 1000 uH, so I'll leave modifying this for another day. 

And, strictly speaking, I didn't need to incorporate a sequencer into the Exciter's design -- I could have used the existing sequencer in the 813 transmitter to perform the same function. But incorporating this sequencer allows me to easily test the Exciter as a stand-alone unit.

    

(Page 3. Click on image to enlarge)

Notes on page 3: 

This is the audio driver which drives the 813 Modulator Deck. Externally, and prior to this stage, I use a Behringer Xenyx 802 mixer/amplifier to amplify and equalize my microphone. 

For 100 percent modulation, the Modulator Deck requires an input level of about 80 volts RMS (when driven with a sine-wave -- this is about 226 Volts peak-to-peak). The simplest way to get this sort of amplitude is with a transformer. On eBay I found an audio output transformer (designed to present to a push-pull driving stage a load of 6.6K or 8K ohms when driving either a 4, 8, or 16 ohm load -- its Part Number is OT20PP), and I decided to connect it in reverse to drive my Modulator Deck so that I could transform the high-impedance of the Modulator Deck input to a low-impedance, and then drive this low-impedance with a speaker amplifier designed to drive loads in the 4 to 16 ohm range. 

To test which combination of input/output windings would work best in my application, I connected the transformer to the Modulator Deck and drove it with a stereo amplifier. With a 1 KHz sine-wave test signal, for full modulation (corresponding to an audio drive of about 80 Vrms into the Modulator deck), I needed about 12 Vpp of drive from the stereo amp. 

For the actual transformer driver, I used an LM1875 speaker amplifier. Its output is single-ended, so, to get 12 Vpp out with some headroom, I used the 26 VDC power supply to power it. 

I also decided to use the 16 ohm tap as the primary (driven by the LM1875) and the 6.6K ohm taps as the secondary (to drive the Modulator Deck). This is the lowest step-up turns-ratio provided by the windings, and the Modulator Deck's input impedance is transformed to be about 5.4 ohms, as measured at the output of the LM1875, which conveniently lies between the LM1875's 4 ohm and 8 ohm load specs. (Any other combination of windings would have resulted in a lower load impedance for the LM1875). 

When driving the Modulator Deck to full modulation, the LM1875 delivers about 3.6 watts into this 5.4 ohm load. 

There is a potentiometer to allow some amount of gain adjustment, but the primary gain is back at the Behringer mixer. And there's a mute circuit to mute the audio drive to the Modulator Deck when the 813 Transmitter is not transmitting. (The 813 transmitter does not like it when the modulator and modulation transformer are driven when the PA deck is not generating RF). 

The low-frequency -3 dB point is about 280 Hz (determined by R28 and C44), which I purposefully added when I discovered that lowering this frequency caused the AM signal to sound a bit fuzzy (due to IMD products related to the voice frequencies below this point). The upper -3 dB point for the exciter/813 rig (combined) is around 4 KHz. These points were measured by driving the modulator with sine-waves and measuring the peak-to-peak envelope of the modulated RF. 

As a precaution against EMI problems involving RF interacting with the audio components, the audio components are all placed within a separate shielded chamber (made using double-sided PCB stock) within the chassis. All signals which transition into this chamber from the area containing the Exciter's RF stages are first filtered using feed-thru caps and L/C (or R/C) low-pass filters.

    

(Page 4. Click on image to enlarge)

Notes on page 4:

1. The 26 VDC power supply is a Cosel 24V supply (adjustable +/- 10%), rated at 4.5 ADC that I picked up from eBay. Now that I've discovered that I don't need 40 watts of RF power, this supply could actually be rated at a much lower DC output current, but hey, hindsight is 20/20.
2. The AC Connector and AC Line filter are actually an integrated modular unit.
3. The VFO is an N3ZI DDS2 VFO. Its output is only about 380 mVpp, so I bump it up to about 2 Vpp (to drive the 'HC86 XOR gates) with an OPA690 op-amp. The 50 ohm resistor in series with the output was added to reduce some high-frequency ringing I had observed, but I'm not sure it's really needed -- I may have been mistaken in this measurement.
4. The VFO Amp is only turned-on when transmitting. With the chassis buttoned-up, I've found that, even though the DDS VFO is always active (even during receive), I cannot hear it on my receiver.
5. The Drain Current meter is 1.5 mA full-scale. The resistors (and sense-resistor) scale the current reading so that the meter represents actual current ÷ 2000.
6. For adjusting the Tank's tuning capacitor, I added an RF tap (R32 and R33) which connects to a BNC on the front panel. The series-2K ohms represented by R32 and R33 help to isolate the tank circuit from the capacitance of coax-cables used to connect this BNC to a scope.
7. And a diplexer is still used to help clean up the Exciter's RF output. The 50 ohm load for the Diplexer's parallel L-C circuit (i.e. the load for out-of-band frequencies) is actually seven 357 Ω, 1/4 watt resistors in parallel. And I placed the series L-C part of the diplexer in a Pomona box because I was concerned that, if not shielded, unwanted RF components would couple around it to the output.

813 Transmitter Wiring Diagram with the K6JCA Exciter installed.

(Click on image to enlarge)

And here are some photos! 

The Audio stage.  Note the shielded compartment. And the LM1875 amplifier attached to the side of the chassis for heatsinking.

(Click on image to enlarge)

In the rack and on the air!

   

(Click on image to enlarge)

(Note: This shot was taken with the FETs powered with 26V, rather than 12V, and a 6 dB attenuator between the Exciter and the PA Deck. With a 12V FET power source, the meter needle is about 0.4 mA (out of 1.5 mA FS), representing about 0.8 Amps of Drain current. 

Additional Notes: 

 Because the tank transformer is 1:1, I wondered what the effect would be if I moved the Tuning Capacitor (C11) from the primary side of the tank to the secondary side. This would allow me to more easily mount the cap, because it no longer would need to float. However, when I performed this experiment, I discovered two issues:

• The tuning range narrowed.
• Output power varied slightly with frequency.

Neither of these outcomes were positive, so I kept the tuning cap on the input side of the tank transformer, and I mounted it on a piece of polycarbonate plastic (from Tap Plastics) to isolate it from the chassis. 

 Resources: 

 Datasheets:

• LM1875 Datasheet
• OPA690 Datasheet
• OT20PP Transformer
• Cosel PAA100F-24 Power Supply

Caveats: 

1. I could have easily have made a mistake, so please regard (and use) this design accordingly. 

2. High voltages can kill. Use caution.

TX Overshoot on Flex 5K

[Additional Notes:

Latest News, 9 MARCH 2011:

Per FLEX, this problem is now FIXED!!!

Gerald's Email to FlexRadio Customers states, in part:

"Fixed ALC overshoot and corrected leveler gain
target in the transmitter audio signal chain.
These changes have been verified by customers
on air and in the FlexRadio lab using a digital
storage oscilloscope to eliminate overshoot."

7 MARCH 2011:

The word from Flex is that they've tested a solution which looks very promising.

Also, additional analysis reveals that the overshoot isn't due to Gibbs Phenomena (as I first hypothesized (see below)), but instead I now believe it's because ALC action occurs before the "real" TX signal is converted to I and Q. Shifting a signal's frequency components each by 90 degrees can result in a time-domain signal whose amplitude exceeds that of the original ALC-limited signal, as demonstrated in the graph below:

(Click on image to enlarge)

Blue Waveform (Sawtooth)
= sin(2πx) + 0.5(sin(2π2x)) + 0.33(sin(2π3x)) + 0.25(sin(2π4x)) + 0.2(sin(2π5x)) + 0.167(sin(2π6x))

Red Waveform (Sawtooth w/components shifted 90^o)
= cos(2πx) + 0.5(cos(2π2x)) + 0.33(cos(2π3x)) + 0.25(cos(2π4x)) + 0.2(cos(2π5x)) + 0.167(cos(2π6x))

[By the way, despite the way it looks, the Red waveform does not have a DC shift. If you examine the equation from which this graph was generated, you'll note that there are only cosine terms in the equation, and that there is no "constant" term, which would represent a DC shift.]

Imagine that the Blue waveform, being our TX signal, had been "normalized" by ALC operation to have a maximum amplitude of 1.0 (i.e. divide all the values in the graph above by 1.5 so that the Blue waveform has a Vpeak of 1.0). The Red waveform, which is the TX signal with its frequency components shifted by 90 degrees, would have a peak amplitude exceeding 1.0 if its components were also normalized by the same amount (divided by 1.5).

And so, to properly limit the signal, ALC must be applied after the conversion from real to complex data. Which, coincidentally, my fix (described below) does.

Interestingly, if a Triangle-wave's components are phase-shifted by 90 degrees, the resultant signal has an amplitude less than the original's amplitude. Which correlates nicely with our observation that we don't see overshoot with a Triangle wave as our signal, but we do if the signal is a Sawtooth wave.

Below is a plot from a MATLAB simulation.  It shows the following:

o  Audio sawtooth waveform, fundamental frequency of 200 Hz and band-limited between 200 and 2400 Hz, and of peak amplitude = 1.
o  Audio sinewave (200 Hz) of peak amplitude = 1 (will be used as reference).
o  The original audio sawtooth waveform, but now with its frequency components shifted by -90 degrees.

o  RF Output, LSB, with 200 Hz tone modulation overlayed (for comparison) on RF LSB waveform with sawtooth modulation (and both shifted +4 to that, when plotted, they won't cover our original audio waveforms).

o  RF Output, USB, with 200 Hz tone modulation overlayed (for comparison) on RF USB waveform with sawtooth modulation (and both shifted -4 to that, when plotted, they won't cover our original audio waveforms).

(Click on image to enlarge)

Note that the Sawtooth's RF waveform has a peak of 1.759 compared to the 200 Hz Tone's RF peak of 1.000, even though both the Sawtooth and the Tone have the same peak audio amplitude of 1.0.  Therefore, if a transmitter were adjusted so that, when driven with the tone, its output was 100 watts (peak), then if the transmitter were driven with a Sawtooth of equal amplitude to the tone, its peak RF output would be 310 watts (i.e. an increase of 4.9 dB in peak power).

And here is the MATLAB code for the simulation, for reference:




clear
clc

% k6jca SSB Modulation Example
%
% Let audio be a 200Hz Sawtooth, of maximum amplitude 1 and band-limited
% between 200 and 2400 Hz.

% Plot 10K points
for inc = 1:100000
    % time tick represents 0.1us.
    % So total simulation time will be 1e-7*1e5 = 10ms. (2 cycles of 200Hz)
    t = (inc-1)*0.0000001;
    x(inc) = t;

    % in-phase sawtooth waveform with frequency components
    % from 200 to 2400 Hz.  And scaled by 1.725 so that peak amplitude is 1.
    i(inc) = (sin(2*pi()*200*t)+ 0.5*(sin(2*2*pi()*200*t))...
         + 0.33*(sin(3*2*pi()*200*t)) + 0.25*(sin(4*2*pi()*200*t))...
         + 0.2*(sin(5*2*pi()*200*t)) + 0.167*(sin(6*2*pi()*200*t))...
         + 0.1429*(sin(7*2*pi()*200*t)) + 0.125*(sin(8*2*pi()*200*t))...
         + 0.1111*(sin(9*2*pi()*200*t)) + 0.1*(sin(10*2*pi()*200*t))...
         + 0.0909091*(sin(11*2*pi()*200*t))...
         + 0.083333*(sin(12*2*pi()*200*t)))/1.7275;
     
    % quadrature generated by shifting in-phase with a 90 degree delay
    % (i.e. subtract pi/2)
    q(inc) = (sin(2*pi()*200*t-pi()/2)+ 0.5*(sin(2*2*pi()*200*t-pi()/2))...
        + 0.33*(sin(3*2*pi()*200*t-pi()/2)) + 0.25*(sin(4*2*pi()*200*t-pi()/2))...
        + 0.2*(sin(5*2*pi()*200*t-pi()/2)) + 0.167*(sin(6*2*pi()*200*t-pi()/2))...
        + 0.1429*(sin(7*2*pi()*200*t-pi()/2)) + 0.125*(sin(8*2*pi()*200*t-pi()/2))...
        + 0.1111*(sin(9*2*pi()*200*t-pi()/2)) + 0.1*(sin(10*2*pi()*200*t-pi()/2))...
        + 0.0909091*(sin(11*2*pi()*200*t-pi()/2))...
        + 0.083333*(sin(12*2*pi()*200*t-pi()/2)))/1.7275;

     % For reference (and comparison) generate a 200 Hz tone of peak ampitude 1
     i_tone_200(inc) = sin(2*pi()*200*t);
     q_tone_200(inc) = sin(2*pi()*200*t - pi()/2);

     % Now let's generate our RF.  First, in-phase.  Frequency is 1 MHz.
     rf_i(inc) = cos(2*pi()*1e6*t);
     
     % quadrature by delaying rf by 90 degrees (subtract pi/2);
     rf_q(inc) = cos(2*pi()*1e6*t - pi()/2);
     
     % Now let's calculate out in-phase and quadrature channels...
     in_phase(inc) = i(inc) * rf_i(inc);
     quad(inc) = q(inc) * rf_q(inc);
     
     
     % ...and then add or subtract them to make LSB and USB
     lsb(inc) = in_phase(inc) + quad(inc);
     usb(inc) = in_phase(inc) - quad(inc);
     
     % For reference, let's also make LSB and USB using the 200 Hz tone,
     % so that we can see if its peak RF differs from the sawtooth's 
     % peak RF
     lsb_tone(inc) = i_tone_200(inc) * rf_i(inc) + q_tone_200(inc) * rf_q(inc);
     usb_tone(inc) = i_tone_200(inc) * rf_i(inc) - q_tone_200(inc) * rf_q(inc);
     
end

top = max(i);
top_q = max(abs(q));

top_lsb = max(abs(lsb));
top_tone = max(abs(lsb_tone));

figure
plot(x,i,x,q,x,i_tone_200,x,lsb_tone+4,x,lsb+4,x,usb_tone-4,x,usb-4);
grid on;
legend('sawtooth (input)','input shifted -90 degrees','200Hz Tone (Reference)','LSB of 200Hz Tone','LSB of sawtooth','USB of 200Hz Tone', 'USB of sawtooth');




My original post is below...]

On the topic of TX overshoot with the Flex 5000...

Last summer a friend of mine mentioned that he was having a problem with PowerSDR and his Alpha amplifier -- it looked to him as though RF overshoots at the Alpha's input were causing it to shut down, and these shutdowns were occurring frequently enough to really annoy him.

I decided to do a bit of investigation. When I looked at the RF envelope from my Flex 5000, I saw overshoots with my 1.18 Console. Thinking that the problem might be related to the software revision, I downloaded the 2.0.7 PowerSDR Console and ran my tests again. Below are snapshots of the OUTPUT RF waveform from my 5000 using the 2.0.7 console.

Oscilloscope is my Tek 2445 that I use to monitor my transmit RF (via an RF-sampler). The two horizontal cursors you see on its CRT mark the peak-to-peak level of the RF signal when the 5000 is in TUN mode and the Tune level is set to 10 watts.

For the following snapshots, PowerSDR is set to:

• Freq: 3.863 MHz
• Mode: LSB
• Drive: 10
• Leveler: Disabled
• TX EQ: OFF
• DX: OFF
• CPDR: OFF
• DEXP: OFF

(Why use 10 watts and not 100? At some point the PA will limit and it won't be able to deliver any additional power. If we run the experiments at high power, we risk having PA-limiting influence our results. But if we run our experiments at low power, we should be able to get a better representation of how high the peaks actually go, because they won't be subjected to PA limiting.)

Anyone can try this experiment with these setting. Here are my results:

First, two nicely behaving waveforms:


Notice how the peaks don't exceed (by much) 10 watts?

But look at these next two. Yikes!



The four snapshots are:

1. Triangle waveform from internal internal software Transmit generator. Looks great!
2. Pulse, from the internal software Transmit generator (at its default settings for Pulse mode). Looks great!
3. Sawtooth waveform from the internal software Transmit generator. Yikes -- it greatly exceeds the 10-watt cursors! Peak power is 49 watts on my LP-100 power meter, yet DRIVE is set to 10 watts.
4. My voice, saying "Ahhh" loudly into microphone. Yikes again! Peak power is about 40-50 watts on my LP-100 power meter, yet DRIVE is set to 10 watts.

Both the "Ahhh" and Sawtooth signals greatly exceed the 10 watt Drive setting on the 2.0.7 console, and the level of the voice signal is very similar to what I'm seeing with my modified 1.18.4 console.

In AM mode, the sawtooth (as modulation) looks exactly as it should, so I don't believe the issue with the sawtooth is that it's somehow "broken."

I thought I'd experiment with the code a bit and see if I could gain further insight...

First, I experimented with the ALC code itself, as my first suspicion was that the overshoot was due to the non-zero attack time. But nope, that wasn't it. I changed the attack time to 0 (so that the ALC was a true peak-detector, and not one with a non-zero attack time), and it made no appreciable difference in the gross overshoots experienced by voice or sawtooth SSB modulation.

I then played around with the location of the ALC algorithm, and the results are very interesting. If the ALC code is prior to the filter_OvSv routine (as it is in the version of code I'm using (v1.18.4) as well as in the SVN 3862 code that I downloaded), then both Voice and Sawtooth waveforms grossly overshoot the target power, per the photos above. In other words, the current ALC code in its current position, in either my console (1.18.4) or in the 2.0.7 console, does not properly limit the output RF for certain waveforms.

However, if I move the ALC code to just after the filter_OvSv routine (and change the buffers used for ALC in newDttSPAGC from buf.i to buf.o), then there is minimal overshoot for all waveforms (Tone, Triangle, Sawtooth, and Voice), and their peaks are all near the target power. In other words, the output RF looks beautiful. [Note: I wasn't able to test the PULSE waveform, because my 1.18 version of the console doesn't have PULSE as one of the options for the test generator].

I'll make a wild guess that the overshoot is due to the bandpass filtering in filter_OvSv and thus similar to Gibb's phenomena. But this is just a guess. Conceptually, it makes sense to me that the ALC processing should be as late in the processing chain as possible, and moving it to just after filter_OvSv seems to be a better place for it than prior filter_OvSv. However, I'll be the first to admit that I don't know what the ramifications are of doing this. Are other problems introduced? I don't know.