(The Great Wave off Kanagawa,by Katsushika Hokusai)
After I had published my previous blog-post demonstrating that source
impedance does not affect SWR on a transmission line (see here), someone reminded me of the three-part series on Wave Mechanics, written by
Dr. Steven Best, VE9SRB, that appeared in QEX magazine in 2001 (the Jan/Feb,
July/Aug, and Nov/Dec 2001 issues), and Walter Maxwell's (W2DU) rebuttal to this
series that appeared in the July/August 2004 issue of QEX.
I recall reading Best's approach at the time and agreeing with it, but I did
not remember reading Maxwell's rebuttal. So why not reread
both?
After finishing Best's three-part series I still agreed with his approach analyzing the wave mechanics as currently-generated waves interacting with waves consisting of an infinite series of past reflections --
it was an approach I've used in a number of my own blog posts (see the list at
the end of this post).
Unfortunately, by the third paragraph of Maxwell's rebuttal it was clear from
his statements that he had misunderstood Best's equations.
(Maxwell's article, "A Tutorial Dispelling Certain Misconceptions Concerning
Wave Interference in Impedance Matching," can be found
here).
Maxwell disputes a number of Best's statements, beginning with Best's
derivation of the equation for Vfwd (the total voltage traveling forward on a
transmission line, whose derivation is represented by equations 6, 7, and 8 in
Part 1 of Best's series), and ending with a refutation of Best's analysis of
the wave interaction that creates a steady-state effective Reflection
Coefficient of 0 (i.e. effective SWR = 1:1) at the input of a T-network tuner.
Best's claim, which he backed up mathematically, is that it is a rearward travelling wave, passing through the tuner from output port to input port, that, when it reaches the tuner's input port, is exactly equal in amplitude but 180 degrees out of phase with the source-voltage's reflection at the T-network's input. These two rearward-traveling waves cancel, and it is this cancellation that causes "the effective
steady-state input impedance to be 50 ohms at the input to the T-network."
On the other hand, Maxwell countered that it is two conjugately-related rearward traveling waves (i.e. one wave is the conjugate of the other -- real components equal, imaginary components having opposite signs, rather than the two waves having equal amplitudes but opposite phases) that, through their interaction, creates a virtual open or short, reflecting all rearward traveling power back towards the load.
Unfortunately, Best did not include any simulations for his T-network example
that would have verified his math and his assertions.
This lack is unfortunate because it is difficult to argue against a mathematical approach if simulations (or better yet, measurements) back it up.
Later in this post, simulations will show that Best's analysis is correct (for example, that the two rearward waves traveling towards the source are equal in amplitude and opposite in phase). But first, I need to tweak Best's Tuner example a bit...
For although simulating Best's T-network tuner system is straightforward using
Simulink, some of the values he chose (e.g. a transmission line
that is 1.2 wavelengths long) make it difficult to discern exactly what is
going on with the reflections and re-reflections on the transmission line.
Let me demonstrate the problem...
First, the Simulink model of Best's T-network system:
Below is a snapshot of the simulated directional coupler Vf and Vr (forward and reverse) voltage
waveforms at the T-network's input port.
Because the reflected voltage is decaying quickly (exponentially) over time,
it is difficult to compare the simulation voltages to calculated
voltages. Where do I place the display's cursors?
But if I were to run a slightly different simulation that generates the
results shown below (where the voltage changes every 4 cycles, rather than
continuously), it is very easy to use the display cursors make voltage
measurements and compare these measurements to calculated results.
The display, above, was created by changing Best's T-network to an L-network
and lengthening the transmission line from 1.2 to 2 wavelengths, extending the
end-to-end travel time. The source's frequency was changed from 21.2 MHz to 10
MHz).
Although I've changed Best's example to allow better comparison with
computed results, it is important to note that the calculated voltage
amplitudes of this new model are the same as those calculated by
Best for his T-network.
But first -- if I am going to compare simulated results to my L-network's calculated values, I need to calculate those values, which means I need to define the system.
And so on to the next step...
L-network Impedance Matching with Mismatched Load:
Consider a lossless transmission line whose length is two wavelengths long,
with a characteristic impedance Zo equal to 50 ohms.
Let the load connected to the line's output be 150 ohms, resistive.
Therefore, in steady-state, the effective impedance seen at the input of the
transmission line is also 150 ohms, resistive, given the two-wavelength
length of the line.
And let there be a lossless, lumped-element L-network at
the input of the transmission line that will transform the 150 ohms
connected to its output port to 50 ohms, as measured looking into the L-network's input port, in steady-state.
This L-network will be implemented as an LC network (series L, parallel C -- note that I will use "L-network" and "LC network" interchangeably in this post)).
At the input and the output of this L-network let us insert directional
couplers that will measure, respectively, the total forward and reflected voltages
at the input of the L-network and the total forward and reflected voltages at the
output of the L-network.
The transmitter driving this network will be represented by a voltage source
of 141.4 VRMS with a source impedance of 50 ohms, resistive.
This transmitter will connect to the L- network's input via a very short
length of 50-ohm coax (in fact, we don't even need this coax, as the
directional coupler, being a lumped-element circuit itself, will still
display the correct Vf and Vr voltages as though there were a transmission
line attached).
Here is the system:
The LC matching network consists of a series 1.1254 uH inductor and a parallel
150.05 pF capacitor which, at 10 MHz, will, in steady-state, transform the 150
ohm load connected to its output port to 50 ohms looking into its input
port.
Calculating the System's Reflection and Transmission Coefficients:
In a transmission line system, Transmission and Reflection Coefficients are
useful for calculating forward and reflected voltages. The figure
below shows the equations for these coefficients when two transmission lines
of different characteristic impedances are connected in series:
Note that for the purposes of the following analysis, these definitions of Transmission and Reflection Coefficients (see
here,
for example) are not a function of the loads that might be
connected at the far ends of the two transmission lines. The
coefficients are solely a function of the impedances immediately at
either side of the impedance discontinuity.
In the LC-network system I have defined, above, there are a total of six
Reflection and Transmission Coefficients.
The load at the far end of the two-wavelength transmission line has one
Reflection and one Transmission Coefficient.
And the LC network, being a two-port lumped-element (i.e. essentially 0
delay) network with a transmission line attached to each of its two ports,
can be represented with two Reflection and two Transmission Coefficients.
These six Reflection and Transmission Coefficient are shown in the figure,
below:
Calculating Load Reflection and Transmission Coefficients:
The load's Reflection and Transmission Coefficients are easily calculated
using the following formulas:
Given Zload = 150 + j0 ohms and Zo = 50 ohms:
Γld = 0.5 + j0
Τld = 1.5 + j0
Calculating LC Network Reflection and Transmission Coefficients:
Equations to calculate Reflection and Transmission Coefficients for a lossless
two-port lumped-element network can be derived using the techniques described
in this blog post:
http://k6jca.blogspot.com/2021/05/lc-network-reflection-and-transmission.html
The general method I use for calculating these Coefficients is described in
the figure, below:
Note that, for the following calculations (which will follow a
point on the transmitted signal as it moves from the transmitter to the load), the impedances that are connected
to either the input or the output port of the two-port network are the
impedances seen
immediately at either port (e.g. the characteristic
impedances of the two transmission lines). These impedances
are
not a function of the impedances connected to the far ends
of the two lines.
Given my example's LC network topology and component values, we can derive
Γ1 and Τ21 (looking into Port 1 of
the two-port LC network) as described, below (note that I've changed the name of Γ11, used in the "general form" described in the previous figure,
to Γ1 for this example) :
Similarly, looking into Port 2 of the two-port LC network, we can
derive
Γ2 and Τ12 using a similar procedure:
Next, given the following values:
-
Transmission lines' characteristic impedances Za and Zb both equal 50
ohms.
- Inductor impedance, Zl, at 10 MHz is + j70.7110 ohms.
- Capacitor impedance, Zc, at 10 MHz is - j106.07 ohms.
We can calculate the LC network's two Reflection Coefficients and two
Transmission Coefficients to be:
Although not necessary for the calculations later in this post, here are
the magnitudes of these four Reflection and Transmission Coefficients:
Calculating Forward and Reflected Voltages:
First, a note regarding voltage names...
I derived my equations, below, independently from Best's articles, without referencing his voltage labels. Later in this post, at the point where I compare Best's calculated voltages to my voltages, there will be a table linking Best's voltage labels to my labels.
Continuing...
Using the three Reflection Coefficients and three Transmission Coefficients
calculated earlier, we can start calculating system forward and reflected voltages.
The system is driven by a gated sine-wave source. To understand how an
infinite series of reflections can build up, let's examine what happens when
this source is first turned on, using a Lattice Diagram to show how a single
point on the Vs waveform moves through the system over time:
Thus, the voltage of each reflection, re-reflection, or transmitted
voltage can be found simply by multiplying the value of the voltage arriving
at the impedance discontinuity by the appropriate Reflection Coefficient or
Transmission Coefficient.
To calculate Vf1: note that the voltage leaving the source impedance
and entering the first transmission line, at the instant it enters this
line, sees the transmission line's characteristic impedance Zo as its
terminating impedance. Thus, the voltage entering the line, Vf1, can
be calculated as a simple voltage divider:
Vf1 = Vs*Zo/(Zo + Zs)
This is true for every point of the Vs waveform arriving at the
Zs-to-transmission line junction.
Therefore, given a Vs of 141.4 volts and a Zs equal to the transmission line's Zo, Vf1 will always be 70.7 volts.
When Vf1 (the forward voltage on the transmission line traveling towards the
LC network's input) arrives at the LC network's input port, it sees an impedance
mismatch represented by Γ1, the LC network's input port
Reflection Coefficient.
Note that this reflection coefficient is a function of the impedance immediately connected to the network's output port (i.e. Zo of the transmission line connected to the port), rather than a function of the impedance at the far end of this same transmission line. This is because the point we are following on the waveform has no "knowledge" of what is at the far end of the line (this is a result of the Principle of Superposition).
In other words, this point on the voltage waveform that we are following is similar to a wave traveling through the ocean which has no knowledge that at the far end there might be a coastline off of which it will reflect. All it sees is the water immediately in front of it through which it is passing.
Continuing...
When this point on Vf1 arrives at the input port of the LC network, part of Vf1 is transmitted back to the source. This reflected
voltage is Vr1, where Vr1 = Vf1* Γ1.
And part of Vf1 continues forward through the LC network to the second
transmission line. This forward-traveling voltage is Vf2, where Vf2 =
Vf1*Τ
21.
The part reflected back to the source, if the source impedance equals the
transmission line's characteristic impedance (as it does in this example), stops there and is not
re-reflected back to the load.
A quick note -- the source voltage, itself, plays no role in the reflection
of a voltage wave arriving back at the source. This reflection is
solely a function of the source impedance, not the source
voltage, and it is an outcome of the Superposition Principle:
Vf2, the part of Vf1 that has continued forward through the LC network and onto the second transmission line,
continues forward on the second transmission line until it reaches the load
mismatch, at which point part of it is reflected back to the source (that
is, towards the output port of the LC network) with a voltage of
Vf2*Γld , and part continues forward into the load (voltage
of Vf2*Tld).
The reflection traveling back from the load, when it arrives at the
output port of the LC network, sees another impedance mismatch, and it will be partially re-reflected back
towards the load (i.e. it will move in the forward direction) with a voltage
of Γ
2*(Vf2*Γ
ld) and partially transmitted through the LC
network towards the source (voltage T
12*(Vf2*Γ
ld)) .
The re-reflection back towards the load will, when it arrives at the
load mismatch, again be partially reflected back towards the LC network and
partially transmitted into the load.
This ping-ponging back and forth on the transmission line between the output
port of the LC network and the load continues ad infinitum. And
every point on the Vs waveform undergoes this ping-ponging.
Thus, in steady-state (after Vs has been on for awhile), if we were to take
a snapshot in time of the reflections and re-reflections at either
ends of the transmission line and the LC network, we would see both the
voltage Vf2 from the source entering the line as well as all of the past
reflections and re-reflections from previous values of Vf2:
There are four important infinite series in the diagram, representing the
past reflections that are still traveling back and forth on the transmission
line at the time of this "snapshot".
By the Principle of Superposition, we know, for example, that the
total voltage traveling forward towards the load on the second
transmission line is the vector sum of all existing voltages
(past re-reflections and present) on the line traveling in this
direction.
Therefore, to calculate these voltages that are a function of ongoing past
reflections, we will need to sum these series.
But before I get to these four infinite series, a quick note on the
exponential terms in the above diagram...
Sidebar on the Propagation Constant e-γl :
The exponential terms that appear in the equations (e.g.
e-γl or e-2γl), after a voltage has
traveled along the transmission line, represent the effect of the
transmission line's Propagation Constant on the voltage's amplitude (i.e. attenuation) and phase.
γ is the propagation constant, and it consists of a real part, α, and an imaginary part, jβ, such that γ = α + jβ.
If we substitute this equation for γ into the exponential, we get: e-γl = e-(α + jβ)l = e-αle-jβl
The real term e-αl expresses how a signal is attenuated along a transmission line of length 'l', while the e-jβl term expresses the phase shift along that same length of line
If we were to take a snapshot in time and compare the voltage Vf at point
A with the voltage Vf at point B, we would see that the voltage at point B
has a negative phase shift compared to the phase of Vf at point A (because
the voltage at point B began earlier in time), as well as some attenuation
due to transmission line loss, per the figure, below:
If the line is lossless, the attenuation factor is 1, and if the line is an
integral number of wavelengths long (as it is in this example), then the
phase shift is 0. In other words, for this example, the propagation
constant equals 1.
The Four Infinite Series:
Examining the earlier "snapshot-in-time" figure, there are four infinite
series. They are defined in the figure, below:
Let's write series-equations for these four infinite-series.
First, Vld, the infinite series representing the voltage across the load:
Next, Vrld, the infinite series representing the voltage reflected back
towards the LC network's output port from the load's mismatch:
Next, Vfld, the infinite series representing the load's reflected voltage
re-reflected back towards the load (i.e. now traveling forwards) by the
LC network's output impedance mismatch:
And finally, Vrs, the infinite series representing the reflected voltage, from
the load, after it has passed backwards through the LC network (output port to
input port) towards the source:
Note that both Vfld and Vrs can be expressed in terms of Vrld (per the last
line in each of the derivations, above). So let's find simpler
expressions for Vld and Vrld. We can then use these simpler expressions
to express Vfld and Vrs.
First, regarding infinite geometric series...
Thus, subject to the restriction noted below, we can reduce Vld and Vrld from
values represented by infinite series to values easily calculated with the
following formulas:
Note that our other two infinite-series, Vfld and Vrs, are simply the Vrld
series multiplied by the appropriate Reflection or Transmission Coefficient:
The figure below summarizes the definitions of the steady-state traveling-wave voltages in the system:
Calculating Steady-state System Voltages:
First, let's state the example's given values:
Zl (i.e. inductor) = 0.0000 + j70.7110
Zc (i.e. capacitor) = 0.0000 - j106.07
Zld (i.e. load) = 150 ohms
e-γl = e-2γl = 1 (propagation
constants)
We can calculate the example's Reflection and Transmission Coefficients:
Next, using the equations developed, above, we can calculate the
following voltages:
Vf1 = Vs*(Zo/(Zs+Zo) = 70.71 volts
Vr1 = Γ1 * Vf1 = 11.7849 +
j33.3316
Vf2 = Τ21 * Vf1 = 35.3537 - j50
volts
Vld = 70.7073 - j100 volts
Vrld = 23.5691 - j33.332 volts
Vfld = 11.7846 - j16.666 volts
Vrs = -11.7841 - j33.3314 volts
Calculating magnitudes of the complex voltages:
Steady-state Total Forward and Reflected Voltages:
The simulations I will present later in this post display forward and
reflected voltages as sampled by two directional couplers (one at the LC
network input port, and the other at the LC network's output port).
These voltages represent the total forward and reflected voltages on a
transmission line at the point in time that the the measurement
is made.
The diagram, below, summarizes the steady-state forward and reflected
voltages on the transmission lines described earlier, and it shows how
voltages traveling in the same direction can be summed to create the
total forward and reflected voltages seen by the two directional
couplers.
Note that summed voltages, above, are vector sums, not amplitude sums, and
thus their values must be calculated at the same point on the transmission
line.
Directional Coupler Forward and Reflected Voltages:
The two directional couplers each measure the total forward voltage (Vf) and the
total reflected voltage (Vr) passing through a point -- they cannot separate
out the different forward waves that might make up these total
voltages.
(Note, though -- although the directional couplers cannot separate out the individual voltages traveling in the same direction that might combine make up a total voltage in steady-state, we can measure these individual voltages during the transient phase when the source is turned on, or off. More on this later, in the simulation section.)
During Steady-state, Vf and Vr are measured by the Directional Coupler at the LC Network's Input
Port, and equal:
- Vf_LC_In = Vf1 = 70.71 volts
- Vr_LC_In = Vr1 + Vrs = 0 volts
Note that Vr_LC_In, the total reflected voltage from the network's input port, is the sum of two voltages.
Similarly, steady-state Vf and Vr are measured by the Directional Coupler at the LC Network's Output
Port, and equal:
- Vf_LC_Out = Vf2 + Vfld = 47.1382 - j66.663 volts
- Vr_LC_Out = Vrld = 23.5691 - j33.332 volts
Note that Vf_LC_Out, the total forward voltage moving towards the load from the output port of the network, is the sum of two voltages.
Magnitudes of these voltages:
|Vf_LC_Out| = 81.65 volts
|Vr_LC_Out| = 40.82 volts
Cancellation of the Reflected Wave to Source:
As I mentioned in the introduction to this post, Best's conclusion is that, in steady state, the reflection of the source voltage off of the LC network's input impedance mismatch (i.e. Vr1) is cancelled by the rearward traveling wave from the load passing through the LC network from output port to input port towards the source (i.e. Vrs).
For Vr1 to cancel Vrs, they need to be of equal amplitude but 180 degrees out of phase, per Best. Let's verify this:
Angle(Vr1) = 70.53 degrees
Angle(Vrs) = -109.47 degrees
Magnitudes are the same. Let's check the difference in angle:
Delta_angle = Angle(Vr1) - Angle(Vrs) = 180 degrees.
Excellent. Amplitudes are identical, and angles are exactly 180 degrees out of phase, as predicted by the math.
Steady-state Total Forward and Reflected Powers:
Calculating steady-state powers, given power delivery by the source of 100
watts:
Total steady-state forward power towards the LC network's input port:
P(Vf_LC_In) = (Vf1^2) / 50 = 100 watts
Total steady-state reflected power from the LC network's input port:
P(Vr_LC_In) = 0 watts
Total steady-state reflected power towards the load:
P(Vf_LC_Out) = (abs(47.1382 - j66.663)^2)/50 = 133.3 watts
Total steady-state reflected power from the load:
P(Vr_LC_Out) = (abs(23.5691 - j33.332)^2)/50 = 33.33 watts
Total steady-state load power:
P(Vld) = (abs(Vld)^2)/Zld = 100 watts
As you can see, steady-state powers are exactly what is to be
expected.
Comparison of Best's T-Network System Voltages with my LC-Network
System Voltages:
The Reflection Coefficients of Best's T-Network and my LC Network have
the same magnitude, but they do not have the same angle.
Therefore, a direct comparison between Best's calculated complex
voltages values and mine cannot be made, because they will have
different phase angles.
However, I can compare the magnitudes of these voltages, using MATLAB to
convert Best's complex numbers to magnitudes, similar to what I did
earlier in this post for my complex voltage values.
The table below contains the magnitudes of the seven voltages named by
Best in his T-Network analysis. To their right I have added my
names for the equivalent seven voltages and the magnitudes that I have
calculated for them:
When expressed as magnitudes, my calculations of system voltages
are identical to Best's. Therefore, any complaints that
Maxwell had regarding Best's analysis and results should also apply to
my analysis.
So let's verify my results via simulation using
Simulink.
Verification through Simulation:
Simulink Model:
The Simulink Model, below, has directional couplers at the input and
output ports of the LC matching network. With these two
directional couplers I can examine forward and reflected voltages
simultaneously at both ports of the LC network.
Note that the forward and reflected voltages at the LC network input
are:
Similarly, the forward and reflected voltages at the LC network output
are:
Drive is from a gated sine-wave. Gating allows display of signal
buildup and decay after the source has been turned on or off, which will
be used to find the values of Vr1, Vrs, Vf2, and Vfld.
Note: the directional coupler model is described
here.
Simulation Goals:
The goals of the simulations are to find the values of Vf1, Vr1, Vf2, Vfld, Vrld, Vrs, and Vload and verify that they match the calculated results.
I will also examine a few of the voltages as they step up (or down) when the source voltage transitions from off to on or from on to off, and verify that the voltage amplitudes at each step are the predicted values.
The Simulink model's Directional Couplers only measure total forward or reflected voltages on a transmission line. If two (or more) voltages are moving in the same direction on a line, the Directional Couplers cannot separate out the individual voltages.
But, by gating the source on or off and having the second transmission line be long enough that it takes 4 cycles for a signal to travel round-trip from the output of the LC network, to the load, and then back again, the Directional Couplers can reveal single voltages during this transient state.
For example, in steady-state, Vr of the Directional Coupler at the input of the LC network is the sum of Vr1 and Vrs. But for the four cycles after the source has just been turned on, Vr is equal to only Vr1, because the reflections that create Vrs have not yet arrived back from the load.
And just after the source is turned off (after being ON for a while), Vr of the Directional Coupler at the LC input is now equal to only Vrs for the first four cycles (before it begins to decay), because Vr1 is now 0.
The figure below demonstrates this:
Similarly, in steady-state, Vf of the Directional Coupler at the
output of the LC network is the sum of Vf2 and Vfwd. And during the first four cycles after the source has been turned on, Vf is solely a function of Vf2. When the source is turned off, the first four cycles of Vf equals Vfld.
The figure below demonstrates this:
Steady-state Voltages:
Let's first look at the mathematically calculated values:
The voltages shown in the figure, below, represent the the system's
steady-state voltages (after the reflection build-ups have essentially
finished). These values were calculated using the equations
developed earlier in this post.
As you can see, the calculated steady-state voltages are:
Vf_LC_Out = Vf2 + Vfld = 81.65 V
Vr_LC_Out = Vrld = 40.82 V
Therefore, we know that:
Let's compare these calculated voltages with the results of the
simulation.
First, though, an important note regarding the voltages shown in the
simulation. The simulated voltages are peak amplitudes, not RMS
values. I chose to use peak amplitudes because these are easily
found using the cursors in the simulation display windows.
Thus, the simulation source voltage Vs is 141.4 Vpeak, rather than
141.4 VRMS, and the cursor readouts will show the same numerical value
as was calculated mathematically using RMS voltages, allowing quick
comparisons between calculated and simulated results.
I will compare voltage magnitudes, only.
Simulated Steady-state results:
First: the steady-state forward and reflected voltages at the LC
network input. These voltages are:
Vf_LC_In (i.e. Vf1) is 70.7 volts, and Vr_LC_In
is 0 volts -- the same amplitudes as were calculated mathematically.
Next, let's look at the steady-state forward and reflected voltages at
the output of the LC matching network. These voltages are:
Vf_LC_Out is 81.6 volts, and Vr_LC_Out (i.e.
Vrld) is 40.8 volts -- again, the same amplitudes as were calculated
mathematically.
And finally, let's look at the steady-state voltage Vload -- the voltage
across the 150 ohm load:
In steady state the load voltage is 122 volts -- essentially the same as
the calculated Vld voltage of 122.5 volts.
Therefore, for Vrld, Vf1, and the four directional-coupler voltages,
steady-state simulated voltages match the calculated voltages.
Voltages at Startup, just after Vs has been gated ON:
As stated earlier, to find the steady-state values of Vf2 and Vr1 we can examine the
voltages of the two directional couplers at startup, after Vs has been
gated ON, and just before reflections from the load have arrived back
at the LC network's output port.
In other words, we can measure Vf2 and Vr1 during the first 4 cycles
of the source voltage Vs being on.
The figure, below, summarizes the these voltages and their calculated
startup amplitudes.
The calculated startup voltages, at the first step of their buildup (or decay) are:
Vf_LC_In = Vf1 = 70.71 V
Vr_LC_In = Vr1 = 35.35 V
Vf_LC_Out = Vf2 = 61.23 V
Vr_LC_Out = 30.62 V
Vld = 91.85 V
Thus, because during these 4 cycles Vr_LC_In = Vr1, and Vf_LC_Out = Vf2, we know that:
Simulated Startup Results:
First, let's examine the startup of the forward and reflected voltages
at the input of the LC network:
Note that Vf_LC_In (i.e. Vf1) always equals 70.7 volts. In other
words, its initial voltage is the same as its steady-state voltage (it
neither builds nor decays).
Vr1 equals the first four cycles of Vr_LC_In, and it measures to
be 35.32 volts.
Note that the measured voltage for Vr1 is the same as its calculated
amplitude.
After these first four cycles Vr_LC_In drops to 8.83 volts due to
the reflection from the load mismatch (traveling backwards
towards the source) finally passing through the LC network from output
port to input port, and destructively summing with the Vr1 reflection
that is also traveling towards the source.
For every additional four cycles Vr_LC_In will continue to step down,
converging on its steady-state value of 0 volts.
The mathematical calculation for this summation, over time (as more
reflections arrive back from the load) is shown as a running sum, below,
on the left-hand side of the figure:
Next, let's compare the simulated startup results for the forward and
reflected voltages at the output of the LC network with their calculated
amplitudes.
Vf2 equals the first four cycles of Vf_LC_Out after Vs is gated
on, and its amplitude is 61.2 volts.
Note that the first four cycles of the other directional coupler voltage,
Vr_LC_Out, equals the first term of the Vrld infinite series as it arrives
at the output port of the LC network from the load. This amplitude
is 30.6 volts. Again, this amplitude is the same as the magnitude of the calculated value of, i.e. | 17.6768 - j25 |.
Vrld's amplitude will continue to step up every 4 cycles, converging on
its steady-state value of 40.8 volts.
Now let's check Vload at startup:
The simulated Vload voltage (starting 2 cycles after Vs is gated on) is
91.8 V for four cycles. This matches the calculated voltage of 91.8
volts.
The amplitude of Vload then steps up to 115 volts for the next four
cycles.
It will continue stepping up every 4 cycles, converging to its
steady-state value of 122 volts.
The calculated Vload amplitudes for the first 3 four-cycle voltage
amplitudes are shown below, on the right-hand side of the figure:

You can see the the simulated amplitudes match the calculated amplitudes.
Therefore, startup simulated voltages match the calculated voltages.
Voltages at Shutdown, just after Vs has been gated OFF:
Finally, the steady-state values of Vrs and Vfld can be found by
examining the directional coupler voltages during the first four
cycles just after the voltage source Vs has been gated OFF (i.e. there
no longer is a drive voltage going to the input of the LC network and
thus there no longer is a Vf1, Vr1, or Vf2).
Calculated results will be compared with simulation results.
The figure, below, summarizes the these voltages and their calculated
startup amplitudes.
Note that Vfld and Vrld, the "continually echoing" forward and reflected
voltages on the transmission line, continue to ping-pong back and forth
between the two ends of the transmission line even with Vs off, but with
each bounce off of an impedance discontinuity their amplitudes diminish.
Let's look at the first step of Vload's decay.
To calculate the first decayed step of Vload, recognize that the
contribution to Vld from the source (i.e. Vf2*Tld) has just
disappeared with Vs being gated off.
Therefore, simply subtract Vf2*Tld (the steady-state
complex value, not zero) from the steady-state complex value of Vld.
This first "decayed" amplitude of Vld calculates to be 30.6 V, which
matches the measurement, above.
Next, let's measure Vrs.
To do this, let's examine reflected voltage at the LC network input,
Vr_LC_In, when Vs is gated off:
First, note that Vf_LC_In, and thus Vf1, is 0 immediately after Vs is gated
off.
With Vf1 equal to 0, Vr1 is also 0, and thus the first 4 cycles of
Vr_LC_In are Vrs, which measures to be 35.3 V, which is the same as its
calculated value.
Finally, let's measure Vfld using the Vf_LC_Out waveform, below:
With Vs now 0, Vf2 is also 0, and therefore Vf_LC_Out equals
Vfld, which measures to be 20.4 volts, equaling the
calculated value of Vfld.
Finally, a quick look at Vr_LC_Out, just to show the decay of this
voltage when Vs is gated off.
Thus, the simulated shutdown voltages match the calculated voltages.
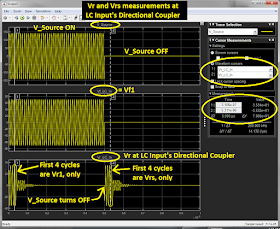
Angle between Vr1 and Vrs:
The mathematics predicts that, in steady-state, the amplitudes of the two voltage waves traveling back to the source, Vr1 and Vrs, will be equal, and they will be 180 degrees out of phase.
The simulation below shows that this is true:
Note that these two measurements are of the steady-state values of Vr1 and Vrs, even though they are taken just after V_source turns on or turns off.
This method of cancellation is an important conclusion, because it validates Best's description of the steady-state wave mechanics at the input of the T network (and in my case, the input of the LC network). The interaction of Vr1 and Vrs, over time, creates a Reflection Coefficient of 0 (at the input port of the T or LC Network) in steady state, due to the cancellation of the steady-state values of Vr1 and Vrs.
In other words, if there is no reflected voltage, as measured by a directional coupler, returning from the input of the T (or LC) network (i.e. the reflected voltage is 0 volts), then the port's Reflection Coefficient must be 0.
Simulation Summary:
To summarize the simulation results: the simulated voltages match the calculated voltages.
I've
included in the table, below, the simulation "capture" (that is, which of the three simulation states (startup, steady-state, or shutdown) and which directional coupler voltage) to identify where each simulation of a calculated voltage can be found:
(Note that this table does not include the simulated Load voltages nor
other voltages not described by Best in his analysis of his T-network,
although these voltages were calculated, verified via simulation, and
described in the simulation section, above).
Conclusions:
I have derived a set of mathematical equations, using Transmission and
Reflection Coefficients representing the LC network and the load,
to calculate forward and reflected voltages at the input and output
ports of an LC impedance matching network that transforms 150 ohms attached
to its output to be 50 ohms looking into its input port.
These equations are used to calculate the values of these voltages from
startup, through the build-up transition, to steady state, and then,
when the source was gated off, the voltages changing from steady-state,
through the decay process, to zero-state.
The amplitudes of these voltages match the amplitudes of the voltages
calculated by Dr. Best for his T-network example in part 3 of his
three-part series.
And these amplitudes are verified via Simulink simulations.
Note that when the voltage source is first turned on, the source's voltage (after it has entered the first transmission line) is reflected by the impedance mismatch at the LC network's input port. This reflected voltage, Vr1, is not 0.
But over time, the voltage traveling back to the source from the LC's input port becomes smaller. This decrease is due Vrld (representing the collection of past rearward traveling reflections from the load), after it passes through the LC network from output port to input port and becomes Vrs, interacting with the LC input port's reflection of the source voltage and cancelling, to some extent, Vr1.
As Vrld increases over time, so does Vrs, increasing the amount of Vr1 being cancelled. And so, over time, the total voltage returning to the source from the input of the LC network converges to 0, the steady-state value.
This growth in cancellation is exactly predicted by the description of the wave mechanics and the equations developed above.
One important conclusion verified by the simulations is that Vr1 and Vrs, in steady-state, have equal amplitudes but are 180 degrees out of phase, so that when they are added, they cancel, and there no longer is a reflected wave traveling back from the LC network input.
Thus, the L-network's input's effective Reflection Coefficient during steady-state is 0.
In summary, the calculated voltages of Dr Best's
T-network system have been verified with Simulink simulations of my L-network system, validating Dr. Best's conclusions regarding the wave
mechanics of a system with an impedance-matching network.
Other Comments:
1. Match Independent from Source Impedance:
In steady-state, the impedance looking into the LC network's input port can be shown mathematically to be independent of source impedance. This conclusion is probably obvious, given that the input impedance of a two-port lumped-element matching network depends solely on the network's components and the load attached to its output port.
But the use of transmission and reflection coefficients to calculate transmission-line system voltages can obscure this fact, given that some of these transmission and reflection coefficients are functions of the source impedance (i.e. Za, as defined below).
Let's use the LC matching network, above, as an example, and let Zin equal the impedance looking into the LC network's input port.
Let Za equal the impedance looking back (towards the source) from the input of the two-port network. In this example, to meet this definition I've defined both the source impedance and the characteristic impedance of the transmission line connecting source to LC network input to be Za.
From Best (part 1, eq. 15):
Zin = V(x)/I(x) = Za * (Vfwd + Vref) / (Vfwd - Vref)
(Note that I have used Za in lieu of Best's Zo because I've defined (above) the characteristic impedance of the transmission line at the LC network's input to be Za, and location 'x' on the first transmission line is defined to be at the end of the line, next to the two-port network's input port).
From earlier in this blogpost I know:
= Τ12 * Γld * Τ21 * Vf1 / (1-Γ2 * Γld )
(assuming e-2γl = 1, which it does for my LC network example)
Substituting the equations for Vr1 and Vrs into the equation for Vref , and substituting Vf1 for Vfwd, then substituting these new equations for Vref and Vfwd into the equation, above, for Zin, and cancelling out Vf1, I get:
Zin = Za*(1+Γ1-Γ2*Γld-Γ1*Γ2*Γld+Τ12*Τ21*Γld)/(1-Γ1-Γ2*Γld+Γ1*Γ2*Γld-Τ12*Τ21*Γld)
The goal is to reduce this large equation so that, hopefully, the Za term disappears (i.e. Zin becomes independent of source impedance).
To do so, however, requires that I express the Transmission and Reflection Coefficients in terms of their underlying impedances. The equation becomes even more complicated!
Fortunately, MATLAB's Symbolic Math Toolbox comes to the rescue. Using it, the equation for Zin (when the load is attached to the output port through a lossless transmission line two wavelengths long) is determined to be:
Zin = Zc + Zl + (Zc^2*(Γld - 1)) / (Zc - Γld*Zc + Zb*(Γld + 1))
where Zc is the capacitor's impedance, Zl is the inductor's impedance, Zb is the characteristic impedance of the transmission line between the LC network's output and the load, and Γld is the reflection coefficient of the load. (For other transmission line lengths, first multiply Γld by the Propagation Constant, e-2γl, appropriate for that length before calculating Zin).
A more general form in terms of a series impedance (Zs) and a parallel impedance (Zp) with a load at the end of a transmission line of characteristic impedance Zb and length l (in wavelengths) is:
Zin_ZsZp = Zp + Zs + (Zp^2*(Γlde-2γl - 1))/(Zp - Γlde-2γl*Zp + Zb*(Γlde-2γl + 1))
Note that Zin is not dependent upon Za!
A Simulink example demonstrates that source impedance does not affect the LC network's effective input impedance (i.e. looking into its input port) during steady-state. This effective impedance remains 50 ohms, resistive, and the reflected voltage at the LC network's input, as measured with a directional coupler referenced to 50 ohms, still goes to 0 during steady-state.
Also, if the voltage source amplitude is adjusted so that 100 watts is dissipated by the load, the amplitudes of the total forward and total reflected voltages on the transmission line between the LC network and the load are the same as the matched source impedance example of this post.
The simulation, below, demonstrates this independence from Source Impedance. Note that both the source impedance and the characteristic impedance of the transmission line connecting source to LC network input have been set to 25 ohms, and the source voltage adjusted so that the power dissipated at the load is 100 watts:
Note that although there is now a mismatch between 25 ohm line and the input of the LC network (so that the actual SWR is no longer 1:1), the directional coupler, measuring at a single point and
referenced to 50 ohms, in steady-state still sees a 50 ohm match at the input of the LC network.
The Load Reflection and Transmission Coefficients have not changed:
Γld = 0.5 + j0
Τld = 1.5 + j0
But the LC network's Reflection and Transmission Coefficients have changed:
Here are the magnitudes of these six Reflection and Transmission Coefficients:
Simulink File:
The Simulink file for my LC Network matching example can be found here:
References:
Best, S., Wave Mechanics of Transmission Lines, Part 1: Equivalence of
Wave Reflection Analysis and the Transmission-line
Equation, QEX, Jan/Feb, 2001
Best, S., Wave Mechanics of Transmission Lines, Part 2: Where Does
Reflected Power Go?, QEX, July/Aug, 2001
Best, S., Wave Mechanics of Transmission Lines, Part 3: Power Delivery
and Impedance Matching, QEX, Nov/Dec, 2001
Maxwell, W., A Tutorial Dispelling Certain Misconceptions Concerning
Wave Interference in Impedance Matching, QEX, July/Aug,
2004
Other Transmission-Line Posts:



















































No comments:
Post a Comment