IMD Uncertainty due to Distortion on Input Test Signal

Several years ago, while I was building my 500 watt solid-state HF Power Amplifier, I created an IMD test system to let me quickly perform two-tone IMD measurements as a function of swept input power (and thus a function of swept output power).

This was after I had discovered that at low to medium transmit levels the PA could have significant IMD (as shown in the image, below), and I needed a way to quickly perform distortion and gain measurements over a broad range of powers while I experimented with improving the PA's performance.

The test system consisted of two HP 3335 generators whose outputs were summed together. The resulting two-tone signal was then amplified to higher power (sufficiently high enough to drive the PA to full output) using an ENI 525LA Linear amplifier that is rated up to 25 watts output with 50 dB of gain.  

 Distortion was measured with an Agilent E4406A Spectrum Analyzer, and the system was controlled via GPIB using a MATLAB program to automate the power-sweeping and distortion measurement (see the link to my HF PA, above, for more info on the test system).

At higher powers the ENI amplifier does introduce its own IMD distortion into its output, but I already had this piece of equipment in my lab, and I decided that for my "one-off" PA design, it made sense to use equipment I already had, rather than try to purchase or build something that might be better performing but more expensive and that I might never use again.

But there is an issue using a test source that introduces its own IMD products.  If the test signal to the PA's input has distortion, these distortion products will interact with the two-tone IMD products created within the PA, with the result that the measured IMD at the PA's output might not represent the PA's actual IMD performance.

The block diagram, below, shows my IMD test system and conceptually describes the problem when IMD is present on the two-tone test signal at the PA's input:

At the time, I did not investigate any further the issue of the effect of source distortion on output distortion, but recently I came upon a thread on the eHam.net Amplifier forum that discussed IMD uncertainty and it prompted me to revisit the issue with respect to my own PA design.  (And more discussion can be found on this eHam thread (started by me):  Calculating IMD Uncertainty).

The Math of IMD Uncertainty:

As I mentioned, above, the two-tone signal (with distortion) from my ENI 525LA amplifier drives the PA.  Thus, the two tones and IMD products from the preceding ENI amplifier are amplified by the PA.  During the amplification process the PA's own non-linearities also create their own distortion products from the two-tone signal being amplified, and these products will sum (in some fashion) with the incoming IMD products from the ENI amp.

(This is a simplified description of what actually is occurring.  In addition to the PA creating distortion from the two-tone signal, there are also distortion products created by the mixing of the incoming distortion products from the ENI amplifier.  I am going to assume that these additional mixing products are at a low enough level to not significantly contribute further to the IMD at the amplifier's output.)

So, as an approximation of how the PA's internally generated IMD products interact with the incoming IMD products from my ENI amplifier, we can say that the PA's measured  Output IMD (as measured on my Spectrum Analyzer) is the sum of the PA's actual IMD (that is generated solely by the two tone test signal) plus the incoming Source IMD (i.e. the ENI amp's IMD ).

Both the measured IMD and the source IMD should be computed in terms of dBc, that is, with respect to the level of either one of the two tones of equal amplitude (if Source IMD and Measured IMD are both referenced to dBc, no additional scaling is required of the source IMD components with respect to PA gain).

If we consider the source and measured IMD components to be voltages, the Spectrum Analyzer is measuring the sum of the two:

The level of V_IMDMeasured will be a function of the amplitudes and phases of V_IMDActual and of V_IMDSource.

The maximum and minimum values of V_IMDMeasured will occur when the phase difference between V_IMDActual and V_IMDSource is either 0 or 180 degrees.

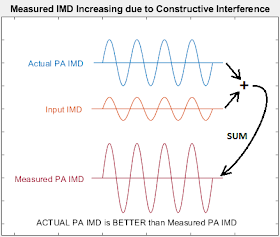
The images below depict a signal increasing in value due to Constructive Interference...

...and of a signal decreasing in value due to Destructive Interference:

Because the amplitude of the resulting signal depends upon the relative phase of the two signals being summed, there are a range of values that V_IMDMeasured could be.  And so V_IMDMeasured no longer represents the PA's actual distortion (V_IMDActual).

But it is V_IMDActual that we are really interested in -- the actual distortion of the PA, not the now-uncertain measured distortion of the PA.

Rearranging the above two equations, we can create two new equations representing V_IMDActual and its worst-case and best-case values as a function the measured IMD and the source IMD.  These two values, representing the best and worst case possibilities of the actual IMD value, bound the region of possible values within which value of the PA's actual IMD could be.

Note two things about the best-case and worst-case equations, above, for V_IMDActual.

First, V_IMDSource is assumed to be less than V_IMDMeasured. (Later in this post I will discuss how the 'best case' equation for V_IMDActual changes for the case when V_IMDSource is greater than V_IMDMeasured.)

Second, note that the above equations are in terms of voltage.  Because my IMD measurements are in dB, it is necessary to convert the results back to dB for comparison purposes.  The following derivation shows how this is done:

Continuing with the derivation:

This last equation is solely in terms of IMD measurements made in dB.  Note that the left hand quantity represents the value that should be added to the measured IMD (in dB) to determine the actual IMD, in dB.

(There is MATLAB code later in this post that describes all of the mathematical steps).

We can also create a plot of the worst-case and best-case values as a function of the difference in signal levels (as either voltage or power) between measured IMD and source IMD.

The plot below graphs the two possible outputs from the equation, above.  Note that the x-axis is the value of "dB_delta",  i.e. the difference between the Source IMD and the Measured IMD. 

The above equations assume the typical case of the Source IMD being less than the Measured IMD (and thus dB_delta is negative).  But this might not be the case.  If Source IMD is greater than Measured IMD, then the Source and Measured terms must be swapped in the 'best-case' equation to prevent the argument of the log() function from becoming negative.  (The 'worst-case 'equation remains unchanged)

Therefore, if Source IMD is greater than Measured IMD, the 'best-case' equation becomes:

An Example:

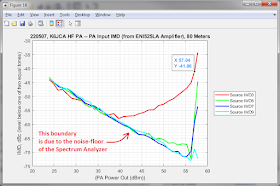
Let us use as an example 80 Meter IMD measurements I made of my HF PA back in 2019:

At the same time, I also captured the IMD characteristics of the two-tone test signal from the ENI 525LA amplifier that was driving the PA's input.  

Note that the power-steps on the x-axis of the two plots, above, are exactly the same -- I generated the Source IMD plot by simply moving the Spectrum Analyzer's input from the PA's output (via a large attenuator) to a directional coupler attached to the PA's input and then I ran exactly the same test sequence (this second path is shown in the test system the block diagram earlier in this post).  

(Using the directional coupler to measure ENI 525LA distortion allowed me to capture any distortion artifacts from the ENI 525LA that might have been caused by an impedance mismatch between the ENI 525LA's output and the PA's input, and therefore not present if I had simply terminated the ENI 525LA's output in 50 ohms.)

With the captured PA input data (i.e. 525LA output) and PA output data I have all the information I need to calculate PA IMD uncertainty.

The plot below shows:

1. Measured PA Output IMD3.
2. Measured PA Source IMD3 (i.e. Input IMD3 to the PA's input from the EN 525LA's Output).
3. Worst-case Actual PA Output IMD.
4. Best-case Actual PA Output IMD.

The plot below is the same as the plot above, but I've added some data points on the four curves that correspond to a PA output of +57 dBm (i.e. 500 Watts PEP).

You can see that at 500 watts out (i.e. 57 dBm), there is almost exactly a 10 dB delta between the measured IMD of the PA and the Source (Input) IMD from the ENI 525LA amplifier.  

And the worst-case value that the actual PA IMD could be is 2.4 dB above the measured value, and the best-case value is 3.3 dB below the measured value (i.e. -3.3 dB) .

(Note that +2.4 dB and -3.3 dB are the values found for a -10 dB difference in signal level on the Uncertainty plot of best and worst case amplitudes versus relative signal level, earlier in this post .)

You can see the delta between measured IMD and worst-case 'actual' IMD increases as power approaches (and exceeds) 500 watts, due to the worsening Source (Input) IMD (yellow line).

Also, you can see that at low levels (i.e. below about 37 dBm output power) the best-case curve looks a bit wonky, and the worst-case curve begins to slope back up.  And you see the best-case curve going above the measured curve.  

Although surprising, this is to be expected, because in this region the measured Source IMD actually goes higher than the measured Output IMD.  But note that in this region we are no longer actually reading valid Source IMD numbers -- the Source IMD products have run into the noise floor of the Spectrum Analyzer, and it is the noise floor we are instead measuring.  

You can verify this by looking at the noise floor values for a given low-power point on the x axis (e.g. at 25 dBm) -- the noise floor of the Input is higher than the noise floor of the Output.  For this reason, I would recommend discounting best-case and worst-case curves at powers below which Source IMD is in the noise floor.

Below are the Best and Worst case IMD plots for my PA's 80 meter IMD3, IMD5, IMD7, and IMD9 distortion products:

Personally, I find the above plot too busy, and it can be difficult to understand what is going on.  So, recognizing that the 'best case' values are not of much use (compared to the worst case values), the plot below shows just the measured PA IMD and the worst-case values that the PA IMD could actually be.

(Note, again, that the worsening IMD at lower powers occurs because the  measured IMD product or the source IMD product has disappeared into the noise-floor of the Spectrum Analyzer).

Matlab Code:

I used MATLAB to generate the above 'uncertainty' plots from data captured with my E4406A Spectrum Analyzer.  Data was captured in terms of dB.

Below are two different methods for calculating the best and worst case IMD values.  Both give the same results.

The first method calculates the best and worst case IMD values using power (i.e. dB).

The second method calculates best and worst case IMD measurements using voltage.  This second method might be more intuitively obvious, but it does involve converting the measurements that were made in dB to volts, performing the appropriate addition or subtraction, and then, when the calculations are finished, converting from volts back to dB.

How the conversion is made from dB to volts (and then back again) is arbitrary with respect to what is chosen as reference power and load resistance.  The only rule is that the same reference power and load resistance that were used to convert from power to voltage must also be used to convert back from voltage to power.

For convenience, I chose dBm as my reference and 50 ohms as my load, simply because there are on-line calculators that allow me to quickly convert from dBm to Vrms and back again, so I could check for errors in my MATLAB calculations by compoaring with calculations I made separately using the on-line calculators.

And I set 0 dBc (i.e. the level of either of the two tones) to be equal to 0 dBm.  Therefore, at the end when I converted voltage back to dB (actually, back to dBm), the final result was identical to power in dBc.

% % *************************************************************
% % Below are two different methods to calculate IMD Uncertainty,
% % given measurable IMD distortion on a two-tone test signal
% % driving a PA-under-test.
% % Both produce the same results.
% % *************************************************************

% Uncertainty Calculation, Method 1 (in terms of dB)
% --------------------------------------------------
% Note that the IMD measurements are in dB.
%
% Calculate Best-case and Worst-case IMD possibilities given an amplifier's
% measured output IMD and the measured IMD of the source driving it.
%
function [BestCaseIMDdB,WorstCaseIMDdB] = IMDuncertainty(IMDsourcedB,IMDoutputdB)
    IMD_delta = IMDsourcedB-IMDoutputdB; % neg. if source IMD < Output IMD
    expTerm = 10^(IMD_delta/20);         % Vsource/Voutput
    % Next, dB of sum of Source and PA-Output IMD voltages,
    % referenced to PA-Output's IMD voltage.
    dB_of_sum = 20*log10(expTerm + 1);
    WorstCaseIMDdB = IMDoutputdB + dB_of_sum;
    if IMD_delta > 0  % Source IMD level > Measured Output IMD level
        dB_of_difference = 20*log10(expTerm - 1);   % delta to Output IMD
        BestCaseIMDdB = IMDoutputdB + dB_of_difference;
    else
        % Source IMD level <= Measured Output IMD level
        dB_of_difference = 20*log10(1 - expTerm);   % delta to Output IMD
        BestCaseIMDdB = IMDoutputdB + dB_of_difference;
    end
end

% Uncertainty Calculation, Method 2 (in terms of voltages)
% --------------------------------------------------
% Note that the IMD measurements are in dB.
%
% Calculate Best-case and Worst-case IMD possibilities given an amplifier's
% measured output IMD and the measured IMD of the source driving it.
%
% In order to calculate voltage from power, the IMD measurements are
% assumed to be in dBm (referenced to 50 ohms), but this definition is
% arbitrary!  The final results would be the same irrespective of
% reference power (e.g. 1 mW), or assumed load resistance (e.g. 50 ohms).
%
function [BestCaseIMDdB,WorstCaseIMDdB] = IMDuncertainty(IMDsourcedB,IMDoutputdB)
    % First assume 0 dBc equals 0 dBm as a convenient, yet arbitrary
    % reference.  Convert powers (measured in terms of dBc, now dBm)
    % to voltages:
    Vsource = (10^(IMDsourcedB/10)*50*0.001)^(1/2); % convert dBm to V
    Voutput = (10^(IMDoutputdB/10)*50*0.001)^(1/2); % convert dBm to V
    Vactual_WorstCase = Vsource + Voutput;
    % convert V to dBm (actually dBc)
    WorstCaseIMDdB = 10*log10((Vactual_WorstCase^2)/(50*0.001));
    if Vsource > Voutput  % Source IMD level > Measured Output IMD level
        % subtract Vouput from Vsource, to keep the log argument positive
        Vactual_BestCase = Vsource - Voutput;
        % convert V to dBm (actually dBc)
        BestCaseIMDdB = 10*log10((Vactual_BestCase^2)/(50*0.001));
    else
        % Source IMD level <= Measured Output IMD level
        % subtract Vsource from Voutput, to keep the log argument positive
        Vactual_BestCase = Voutput - Vsource;
        % convert V to dBm (actually dBc):
        BestCaseIMDdB = 10*log10((Vactual_BestCase^2)/(50*0.001));
    end
end

Note:  If you are viewing the code on a small screen, you might not be able to see the full length of the lines of code.  In this case, cut-and-paste the code into an application with a larger viewing pane (e.g. Notepad, Word, etc.).

Resources:

These two application notes discuss IMD Uncertainty (as it relates to Spectrum Analyzer IMD measurements and IMD generated within the Spectrum Analyzer, itself):

Interaction of Intermodulation Products between DUT and Spectrum Analyzer, Rohde & Schwarz

Dynamic Range Optimization for Distortion Measurements, Keysight Technologies

Standard Caveat:

As always, I might have made a mistake in my equations, assumptions, drawings, or interpretations.  If you see anything you believe to be in error or if anything is confusing, please feel free to contact me or comment below.

And so I should add -- this information is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE.