For those of you who would rather jump to the new L-Network equations rather than dive into their derivation, below, please go here:
***********************
- Jeff, K6JCA 7 April 2015
The selection of one L-network configuration over another (series-parallel versus parallel-series) is typically based upon a relationship between the load impedance's resistance and the "target" resistance that the load is to be transformed to.
Note that the load itself need only be characterized in terms of its resistance (Rload) to determine if a series-parallel or parallel-series L-network should be selected, even if the load represents a complex impedance (i.e. Zload = Rload + jXload).
These constraints are commonly defined to be:
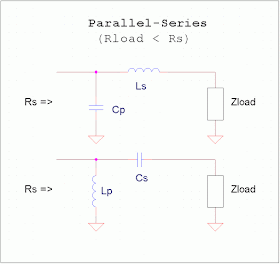
- Apply parallel-series L-networks if Rload < Rs
- Apply series-parallel L-networks if Rload > Rs
But are these two constraints correct?
Let's examine them...
The four most typical L-networks are shown below, along with their
commonly-defined constraints. So, the constraint for selecting the
Series-Parallel LsCp or CsLp L-networks is Rload > Rs, and the constraint for the Parallel-Series CpLs or LpCs L-networks
is Rload > Rs.
(click on image to enlarge)
The two constraints I've defined above are what I call the "classical"
L-network constraints, in the sense that they can be found throughout the
literature on impedance matching. The two Smith Charts, below, show
the range of impedances associated with each constraint, i.e. the range of
impedances that satisfy Rload < Rs and the range of impedances that satisfy Rload > Rs.
Note that the two Smith Chart regions are mutually exclusive and
therefore do not overlap.
The first Smith Chart shows the impedances (in the red area) that meet
the Rload < Rs constraint. And per the "classical" definition of this
constraint, these impedances can be matched with a Parallel-Series
L-network.
The second Smith Chart shows the impedances (in the yellow area) that meet the Rload > Rs constraint. And per the "classical" definition of this constraint, these impedances can be matched with a Series-Parallel L-network.
Below is an example of one such a statement. (My comments are in
red).
Instead (as I will derive later in this post), the constraints
for selecting Series-Parallel and Parallel-Series L-networks actually
are:
- Apply parallel-series networks when Rload < Rs
- Apply series-parallel networks when Gload < 1/Rs
Note that Yload
= Gload
+ jBload, where Gload = Rload / (Rload2 + Xload2) and Bload = - Xload / (Rload2 + Xload2).
In the figure below are two common Parallel-Series L-networks, CpLs and LpCs. (I will mention two other Parallel-Series L-networks, LpLs and CpCs, later in this post.)
Viewed on a Smith Chart, the Zload impedance "space" representing Rload < Rs has not changed from our original discussion, above, and it still
looks like:
And in the figure, below, are two common Series-Parallel L-networks,
LsCp and CsLp. (I will mention two other networks, LsLp and CsCp,
later in the post).
With the new Gload < 1/ Rs constraint for Series-Parallel
networks, the impedances that can be matched with a Series-Parallel
network now look like:
In other words, in the above diagram, depending upon where Zload lies on the Smith Chart, a Series-Parallel L-network consisting of either an LsCp or a CsLp network will transform Zload to Rs.
The Overlap of Rload < Rs and Gload < 1/ Rs:
If you examine the two Smith Charts, above, you can see that the Rload < Rs region and the Gload < 1/ Rs region are no longer mutually exclusive; they now partially overlap.
Load impedances within this 'overlap' area can be matched to Rs with
either a Series-Parallel or a Parallel-Series L-network,
as the Smith Chart, below, shows (the overlap area is shown in light
green).
You can see that in the top 'light green' area, either an LpCs or an LsCp network can transform an impedance to be Rs.
And in the bottom 'light green' area, either a CpLs or a CsLp network can
transform an impedance to be Rs.
For the sake of completeness, let's examine the subset of the region of
the Rload < Rs Smith Chart space where it does not overlap
the Gload < 1/ Rs space (i.e. this subset spans the region in which Gload > 1/ Rs). The matching L-network is still a Parallel-Series network (CpLs
or LpCs):
Similarly, let's examine the subset of the region of the Gload < 1/ Rs Smith Chart space where it does not overlap
the Rload < Rs space (i.e. this subset spans the region in which Rload > Rs). The matching network is still a Series-Parallel network (CsLp or
LsCp).
The table below summarizes which L-network to use depending upon Zload's characteristics:
L-Networks Consisting only of Two Inductors or of Two Capacitors:
Finally, there are four more L-network cases that should be
mentioned: two L-networks that consist solely of two capacitors and
two that consist solely of two inductors. These can be configured as
CpCs, CsCp, LpLs, or LsLp networks:
To summarize, these new constraints are universally applicable to all
eight L-network configurations:
Let's now look at the Parallel-Series and Series-Parallel L-network design equations and their derivation. And in doing so, I will point out the common flaw in the Series-Parallel derivation that resulted in the incorrect Rload > Rs constraint and how to derive the correct Gload < 1/ Rs constraint.
Deriving the Parallel-Series Network Equations:
Let's first derive the design equations for the Parallel-Series L-network -- these equations can be used to find the L-network component values for a specific impedance transformation.
We can draw a general form of this network with the parallel element
a susceptance B and the series-element a
reactance X. (Note that both of these elements are
assumed to be lossless, For lossy networks, see this blogpost:
New Equations for Lossy L-Networks.)
The load is complex: Zload = Rload + jXload. And we want to transform it to be a resistance equal to Rs.
The impedance looking into the network, Zin, is:
Zin = 1 / (jB + (1 / (Rload
+ j(Xload
+ X))))
Let's expand this further...
Zin = (Rload
+ j(Xload
+ X)) / (1 + jBRload
- B(Xload
+ X))
Our goal is to select B and X such that Zin = Rs. In other words:
Rs = (Rload
+ j(Xload
+ X)) / (1 + jBRload
- B(Xload
+ X))
We can expand this equation and then separate out the equation's real terms and the imaginary terms. If we do, we get the following:
Equating the Real terms:
Rs - Rload
= BRsXload
+ BRsX
Equating the Imaginary terms:
X = BRsRload
- Xload
We can take that last equation, plug it into the X term of the previous equation, and solve for B. The resulting equation will be in quadratic form and therefore has two solutions. Each of these two solutions for B can then be plugged into the equation for X (the last equation above). The final results are two B, X pairs:
Solve for B and X, then convert the resulting reactances and susceptances into actual inductors and capacitors. Note:
- If B is negative, the component will be a shunt inductor
- If B is positive, the component will be a shunt capacitor
- If X is negative, the component will be a series capacitor
- If X is positive, the component will be a series inductor
- shunt-inductor, series-inductor (LpLs)
- shunt-inductor, series-capacitor (LpCs)
- shunt-capacitor, series-capacitor (CpCs)
- shunt-capacitor, series-inductor (CpLs)
Deriving the constraint
Rload
< Rs:
Note the term Rs-Rload under the square root sign. This term must be not be negative for the answer to exist.
Note the term Rs-Rload under the square root sign. This term must be not be negative for the answer to exist.
In other words, the following condition must be met:
Rs ≥ Rload
However, it can be easily shown that if Rs = Rload, the solution is not a two-element L-network but a single series reactance.
Therefore, for two-element L-Network solutions, we will only
consider the cases in which Rs-Rload is greater than 0.
And thus, setting Rs-Rload to be greater than 0 and then rearranging it,
we have our constraint for parallel-series networks:
Deriving the Series-Parallel Network Equations (Method 1, the Classical approach):
In a fashion similar to our analysis of parallel-series networks, we can draw a general form of the series-parallel network, with the series-element a reactance X and the parallel element a susceptance B. (Again, both of these elements are assumed to be lossless, For lossy networks, see this blogpost: New Equations for Lossy L-Networks.)
Again, Zload = Rload + jXload. And again we want to transform the load impedance to be a resistance equal to Rs.
The impedance looking into the network, Zin, is:
Zin = jX + 1 / (jB + (1 / (Rload
+ jXload))
Again, I'll set Zin equal to our target resistance, Rs. Expanding the above equation and then separating out the resulting real and imaginary terms, we get:
Real terms:
B(XRload
-
XloadRs) = Rload
- Rs
Imaginary terms:
X = (BRsRload
-
Xload) / (1 - BXload)
The real-term equation can also be solved for X:
X = 1/B + (XloadRs)/Rload
- Rs/(BRload)
Through X, we can now equate this last equation to the previous one and solve for B. Again, the results for B are in the form of a quadratic equation whose solutions are two roots, as shown in the equation below. These two roots, when calculated, are then substituted into the second equation below (which is our equation for X, from above):
The results are again two pairs of susceptances and reactances that can then be converted into actual component values. Note:
- If B is negative, the component will be a shunt inductor
- If B is positive, the component will be a shunt capacitor
- If X is negative, the component will be a series capacitor
- If X is positive, the component will be a series inductor
- series-inductor, shunt-inductor (LsLp)
- series-inductor, shunt-capacitor (LsCp)
- series-capacitor, shunt-capacitor (CsCp)
- series-capacitor, shunt-inductor (CsLp)
The next step is to define under what conditions the above equations give
valid solutions, and
this is where this derivation often takes a wrong turn!
The classical approach will typically state that the quantity under the
second square root (i.e. Rload2 + Xload2 - RsRload) must be positive and that this condition is met when Rload > Rs.
As it turns out, Rload2 + Xload2 - RsRload is positive when Gload < 1/Rs, which encompasses a larger range of impedances than those encompassed by
the original "classical" constraint of Rload > Rs.
Let's prove this conclusion mathematically...
Deriving the constraint Gload < 1/Rs:
The equation under the second square root sign in the equation for B is:
Rload2 + Xload2 - RsRload
And has been stated, this equation must be not be negative for the equations' results to exist.
Thus, we have the equation:
Rload2 + Xload2 - RsRload ≥ 0
However, it can be shown that if the above equation equals zero, the matching network is not a two-element L-Network but a single shunt susceptance. If we ignore this special case, the above equation becomes:
Rload2 + Xload2 - RsRload > 0
Rearranging this equation, we have our new constraint for series-parallel
networks:
Note at the complexity of the derivation of the Series-Parallel set of
equations compared to the earlier derivation of the Parallel-Series
equations. Given the symmetry between the two "match spaces" when
plotted on a Smith Chart, is there were a way to derive the Series-Parallel
equations in a less complicated way?
Deriving the Series-Parallel Network Equations (Method 2, the
Admittance Approach):
Let's use the following diagram for a Series-Parallel L-network and redefine
the input and output impedances to instead be admittances.:
This drawing is equivalent to the series-parallel diagram earlier in the post, except now the load is expressed as an admittance.
And rather than writing an equation for Zin, the impedance looking into the network, I'll instead write an equation for Yin, the admittance looking into the network.
The equation for Yin is:
Yin = 1 / (jX + 1/(Gload + j(Bload + B)))
If I expand this equation and then equate the imaginary terms on either side of the "equals" sign and then do the same with the real terms in the equation, I get the following two equations:
Real terms:
Yin - Gload = YinX(Bload + B)
Imaginary terms:
B = YinXGload - Bload
If I plug this last equation into the previous one and solve for X, we'll again get a quadratic equation. The equations representing the two roots of this quadratic equation can then be plugged into the X term in the equation above for B. The results will be two X,B pairs:
(Note the similarity in form with the parallel-series equations derived
earlier.)
Recall that our target impedance for Zin was the resistance Rs. Yin is just the reciprocal of Zin and so our target is its conductance 1/Rs -- when solving these equations, this is the value you'd substitute into Yin.
Again, for the solutions to exist, the terms under the square root sign must not be negative. And again, ignoring the special case of Yin = Gload (in which the matching network is a single shunt susceptance, not a two-element L-Network), the equations' constraint becomes:
Not surprisingly, this is the same constraint that we found for the earlier series-parallel network analysis. But note how much simpler the design equations are.
If you'd like to verify that both sets of equations produce the same results, keep in mind that:
Gload = Rload
/ (Rload2 + Xload2)
and
Bload = - Xload
/ (Rload2 + Xload2)
More Interesting Facts
Given the new constraint for series-parallel networks (Gload < 1/Rs), these equations allow the entire Smith Chart to now be analytically "matched" to a target impedance with just a pair of networks.
If physically realized, a simple toggle-switch can select the appropriate network for the appropriate Smith Chart region. For example, a switch-selectable LsCp -- CpLs network pair can span the Smith Chart, as can a switch-selectable CsLp -- LpCs pair of networks:
Here are the regions covered by the CsLp -- LpCs pair. One network spans the yellow region, the other spans the non-yellow region.
(click on image to enlarge)
And here are the regions covered by the LsCp -- CpLs pair:
(click on image to enlarge)
If I'd used the original constraints (specifically Rload > Rs for series-parallel networks) to select networks for, say, a computer-driven analysis of matching networks as the load is rotated around a Smith Chart's "circle of constant SWR" (as I did in this post: L-Networks ), there would be a large swath of the circle where I would be missing networks.
For example, suppose I wanted to analyze component values required for a CsLp -- LpCs switch-selectable network. I won't have calculated matching networks for the entire bottom part of the chart because, if I use the original constraints, neither network will create a match for impedances within that area!
(Click on image to enlarge)
(Note the same issue exists for the LsCp/CpLs duo, but in this case the top part of the Smith Chart cannot be matched by the CpLs configuration.)
Of course, in actual life this isn't the case. If I built the networks, I would find that they covered the entire constant-swr circle. The fact that an analysis missed part of the circle is solely due to the incorrect constraint used for the analysis. And if we instead used the correct constraint, Gload < 1/Rs, our analysis would be fine.
Examples of incorrectly derived Series-Parallel constraints:
The following websites incorrectly derive the constraint for applying Series-Parallel L-networks. Below are several examples.
http://www.ece.msstate.edu/~donohoe/ece4333notes5.pdf
http://www.ittc.ku.edu/~jstiles/723/handouts/section_5_1_Matching_with_Lumped_Elements_package.pdf
https://uspas.fnal.gov/materials/10MIT/Lecture11.pdf
(A number of other sites skip the derivations, but still incorrectly state the the Series-Parallel network should be used when Rload > Rs and the Parallel-Series network should be used when Rload < Rs).
My Related Posts:
A quick tutorial on Smith Chart basics:
http://k6jca.blogspot.com/2015/03/a-brief-tutorial-on-smith-charts.html
Plotting Smith Chart Data in 3-D:
http://k6jca.blogspot.com/2018/09/plotting-3-d-smith-charts-with-matlab.html
The L-network:
http://k6jca.blogspot.com/2015/03/notes-on-antenna-tuners-l-network-and.html
A correction to the usual L-network design constraints:
http://k6jca.blogspot.com/2015/04/revisiting-l-network-equations-and.html
Calculating L-Network values when the components are lossy:
http://k6jca.blogspot.com/2018/09/l-networks-new-equations-for-better.html
A look at highpass T-Networks:
http://k6jca.blogspot.com/2015/04/notes-on-antenna-tuners-t-network-part-1.html
More on the W8ZR EZ-Tuner:
http://k6jca.blogspot.com/2015/05/notes-on-antenna-tuners-more-on-w8zr-ez.html (Note that this tuner is also discussed in the highpass T-Network post).
The Elecraft KAT-500:
http://k6jca.blogspot.com/2015/05/notes-on-antenna-tuners-elecraft-kat500.html
The Nye Viking MB-V-A tuner and the Rohde Coupler:
http://k6jca.blogspot.com/2015/05/notes-on-antenna-tuners-nye-viking-mb-v.html
http://k6jca.blogspot.com/2018/08/notes-on-antenna-tuners-drake-mn-4.html
Measuring a Tuner's "Match-Space":
Measuring Tuner Power Loss:
I could have easily made a mistake anywhere in this blog post. If something looks wrong, is unclear, or doesn't make sense, please feel free to contact me!



























ReplyDeleteThank you for this informative post! It’s clear you put a lot of effort into it, and it shows!