Recently I've become interested in Antenna Tuners and I want to post some
notes on them to this blog. I thought that I'd start off these posts
with a quick Smith Chart review/tutorial, given its usefulness in
understanding and analyzing impedance-matching.
But before I start, some assumptions on my part...
I am assuming the reader has a basic understanding of the following:
Why Smith Charts?
Here are a few reasons why Smith Charts are useful...
First, a Smith Chart can represent any complex impedance (e.g. R + jX) or admittance that has a positive real component as a point within a circle of radius equal to one, even if R or X are enormous. So, if plotting a range of impedances that span a wide range of values, these impedances can easily be plotted within the area bounded by the unit circle, rather than across a potentially infinite area.
Note that this transforming of the right-hand side of the infinite impedance plane into a unit-circle is done via the Reflection Coefficient equation (to be introduced just a bit further down).
But how do we interpret the mapped values in (and on) this Unit Circle of Reflection Coefficients?
This is the second reason for using a Smith Chart (and possibly the most important reason). A Smith Chart is an overlay that, when placed upon the Reflection Coefficient Unit Circle, maps a Reflection Coefficient value (as would be measured with a Vector Network Analyzer, i.e. S11 or S22), into the corresponding R+jX impedance or G+jB admittance.
And a third reason why Smith Charts are useful -- Smith Charts provide an intuitive way to understand how matching networks perform their impedance transformations.
The Smith Chart's Foundation: the Reflection Coefficient:
The foundation of the Smith Chart is a calculated quantity known as the "Reflection Coefficient." The Reflection Coefficient (usually symbolized with Γ, the Greek "Gamma"), is a measure of impedance mismatch between a load impedance (Zload) and a desired target impedance (the target impedance is typically the Characteristic Impedance, Zo, of a transmission line, but it could also be the the desired impedance that you might want to transform another impedance to be). For this discussion I will use 50 ohms as our target impedance.
The Reflection Coefficient can be calculated with this formula:
Note that Zload is a complex quantity with both real and imaginary parts:
Therefore, Γ is also a complex quantity, but it is unitless.
Let's look at an example. Consider the following load impedance:
Its impedance mismatch (as represented with its Reflection Coefficient) from our target impedance of Zo = 50 ohms calculates to be:
And we can plot its position (using Cartesian coordinates) on the complex plane:
In addition to expressing Γ's position on the complex-plane using Cartesian coordinates, we can also express its position in terms of Polar-coordinates using rho (symbol: ρ), representing the magnitude of Γ, and theta (symbol: θ), the angle it subtends from the positive x-axis.
Again using our example of the Reflection Coefficient for Zload = 50 + j200 (i.e. Γ = 0.8 + j0.4), this Γ, in Polar coordinates (rho, theta), would be:
where ρ = 0.894 and θ = 26.6 degrees:
Let's plot some more Reflection Coefficients on our Complex plane. I'm going to chose eight more values for Zload, all with a resistance (i.e. "real") value of 50 ohms, and various reactance (i.e. imaginary) values, and then use Excel to calculate Γ:
Here's how these eight Reflection Coefficients look when plotted on the Complex plane:
If we remove the annotation from the image above, our points look like this:
Looks like they form a crude circle, doesn't it?
Circles of "Constant Resistance":
If we calculate Γ for all possible Zloads of 50 ohms resistive and anything reactive, that is, Zload = 50 + jX, where X ranges from -∞ to + ∞, and we add these values to our plot of Γ above, it would become:
It's a circle! This is a circle of "constant resistance". That is, it is the locus of all possible Γ values calculated from the equation Zload = 50 + jX, where R, the resistance of Zload, is fixed at 50 ohms.
Now, if we were to calculate Γ for all possible values of Zload = R + jX, in which X ranges independently from -∞ to + ∞ and R ranges from 0 to + ∞, and then we plotted the results on the complex plane, they would plot into a region bounded by (and including) a circle of radius 1.0, centered at 0,0:
Let's add a few more "constant resistance" plots of Γ to our plot of Γ for Zload = 50 + jX. I'll chose Zload = 150 + jX and Zload = 16.67 + jX, where again, X ranges from -∞ to + ∞:
We have three circles, each circle representing Γ for a Zload with "constant" Resistance and all possibilities of Reactance.
Moving Along a Circle of Constant Resistance:
Lets look at what happens to our plot of Γ if we add additional series Reactance (either inductive or capacitive) to an existing value of Zload. I'll again use the example of Zload = 50 + j200.
First, let's put Γ for Zload = 50 + j200 on our "Resistance" circle:
What happens if we add series reactance? We are creating a new Zload:
When we add jX to our Zload, we are going to move Γ along our "resistance" circle. The movement will be clockwise if we add inductance and counter-clockwise if we add capacitance. If we add just enough series capacitance to our "j200" term, we will cancel it out and be left with Zload = 50 + j0, a perfect match. But if we add too much capacitance, we will continue to move counter-clockwise away from that point of perfect match. To illustrate these points:
We can plot the same movement for an impedance with a negative reactance. For example, consider Zload = 50- j200 ohms...
How does the value of the reactance we're adding correlate to the amount Γ moves along the circle?
We are adding a series reactance to Zload. What happens if I add a series-element that is a short circuit (zero ohms)? Nothing happens -- Γ doesn't move (that is, the impedance at that point doesn't change). So if I add a series element that has a very small reactance, that is, it looks almost a short circuit (such as a large capacitor or a small inductor), there should be little movement along the circle.
In contrast, the more the series element looks like an open-circuit (that is, the higher its reactance, e.g. small capacitor or large inductor), the greater will be Γ's movement around the circle.
(Also note that in the plot above, Γ at its limit (when jX is either -j∞ or +j∞) is at coordinate 1,0, on the circumference of the unit-circle.)
Plotting Admittance in lieu of Impedance:
But suppose we add reactance in parallel with Zload, rather than in series as was done above? How do we visually represent this?
First, recognize that any representation of Zload impedance in series form (i.e. R + jX, where R is resistance and X is reactance) can be transformed into an equivalent parallel form in which:
Where Y is Admittance, G is Conductance, and B is Susceptance.
Yload is simply 1/Zload. Therefore, G and B can be easily calculated by inverting the equation for Zload (Zload = R + jX) which results in these two equations:
Let's calculate the equivalent Yload admittances for our example of nine impedances (all with R = 50 ohms) and add them to the table that's earlier in this post:
The first thing you should note: although R = 50 for all nine values, G is not constant. But take a look at G when Zload = 50 + j0 (our ideal match). It's equal to 0.02 Siemens.
So...what happens to Γ if, say, we hold Yload's Conductance (G) constant but vary Yload's Susceptance (B)?
As an example, what happens if we fix G at 0.02 Siemens? Let's calculate Γ for nine different Yloads, each with its G term set to 0.02 Siemens:
Plotted on the complex plane, the coordinates for these 9 Γ are:
Now, again with G fixed at 0.02 Siemens, let's plot Γ for Yload = 0.02 + jB, where B ranges from -∞ to + ∞:
This is a circle of "constant conductance" (in this case, G = 0.02). Note that it looks exactly like the circle of "constant resistance" that we drew above for Zload = 50 + jX, except this new circle is shifted to the left-hand side of the complex-plane.
Moving Along a Circle of Constant Conductance:
Adding either inductance or capacitance in parallel with Zload moves us along this circle. Adding inductance will move us counter-clockwise and adding capacitance moves us clockwise.
How does the value of the reactance we're adding correlate to the amount Γ moves along the circle? We are adding a parallel reactance across Zload. What happens if I add a parallel-element across Zload that is an open circuit (infinite ohms)? Nothing happens -- Γ doesn't move (that is, the impedance at that point doesn't change). So if I add a parallel element that has a very large reactance, that is, it looks almost an open circuit (such as a small capacitor or a large inductor), there should be little movement along the circle.
In contrast, the more the parallel element looks like a short-circuit (that is, the lower its reactance, e.g. large capacitor or small inductor), the greater will be Γ's movement around the circle.
(Also note that in the plot above, Γ at its limit (when jB is either -j∞ or +j∞) is at coordinate -1,0, on the circumference of the unit-circle.)
For the sake of symmetry (because we did it above for circles of "constant-resistance"), let's add two more "constant-conductance" circles to the one above:
And let's add our previous Γ plots of circles of constant-resistance:
Arcs of Constant Reactance and of Constant Susceptance:
In addition to Γ plots of circles of constant-resistance or circles of constant-conductance, I could also plot Γwith Zload's reactance term (X) held constant and varying R from -∞ to + ∞, or I could plot Γwith Yload's susceptance term (B) held constant and varying G from -∞ to + ∞). The resulting curves would not be circles, though. Let's look at them:
Here are plots of Γ in the complex-plane with R held constant (circles) and with X held constant (arcs of circles):
We have already discussed the circles of constant-resistance. The additional non-circle curves are actually arcs of circles, and they represent the segments of constant-reactance (or constant-susceptance when using admittance) circles that lie within the Smith Chart's underlying "unit circle".
We can plot these arcs by holding X constant and varying R from 0 to infinity (or, for admittance, by holding B constant and varying G from 0 to infinity).
For example, here's a plot showing the Reflection Coefficient (Gamma) for five different impedances, all of which have +200 ohms as their reactance:
If I were to plot all of the impedance which have X = +200 ohms, I would get the following arc of a circle:
(Note that the circle of "constant reactance," above, extends beyond the Smith Chart boundary. The impedances represented by the reflection-coefficients beyond the unit circle have negative resistances. For example, an impedance of -200 + j200 ohms would have a reflection coefficient equal to 1.24 + j0.32.)
But before I start, some assumptions on my part...
I am assuming the reader has a basic understanding of the following:
- Ohms Law
- Impedance expressed as a complex number (R + jX)
- Complex numbers and their math (addition, subtraction, multiplication, and division)
Why Smith Charts?
Here are a few reasons why Smith Charts are useful...
First, a Smith Chart can represent any complex impedance (e.g. R + jX) or admittance that has a positive real component as a point within a circle of radius equal to one, even if R or X are enormous. So, if plotting a range of impedances that span a wide range of values, these impedances can easily be plotted within the area bounded by the unit circle, rather than across a potentially infinite area.
Note that this transforming of the right-hand side of the infinite impedance plane into a unit-circle is done via the Reflection Coefficient equation (to be introduced just a bit further down).
But how do we interpret the mapped values in (and on) this Unit Circle of Reflection Coefficients?
This is the second reason for using a Smith Chart (and possibly the most important reason). A Smith Chart is an overlay that, when placed upon the Reflection Coefficient Unit Circle, maps a Reflection Coefficient value (as would be measured with a Vector Network Analyzer, i.e. S11 or S22), into the corresponding R+jX impedance or G+jB admittance.
And a third reason why Smith Charts are useful -- Smith Charts provide an intuitive way to understand how matching networks perform their impedance transformations.
The Smith Chart's Foundation: the Reflection Coefficient:
The foundation of the Smith Chart is a calculated quantity known as the "Reflection Coefficient." The Reflection Coefficient (usually symbolized with Γ, the Greek "Gamma"), is a measure of impedance mismatch between a load impedance (Zload) and a desired target impedance (the target impedance is typically the Characteristic Impedance, Zo, of a transmission line, but it could also be the the desired impedance that you might want to transform another impedance to be). For this discussion I will use 50 ohms as our target impedance.
The Reflection Coefficient can be calculated with this formula:
Γ = (Zload - Zo) / (Zload + Zo)
Note that Zload is a complex quantity with both real and imaginary parts:
Zload = R + jX
Therefore, Γ is also a complex quantity, but it is unitless.
Let's look at an example. Consider the following load impedance:
Zload = 50 + j200
Its impedance mismatch (as represented with its Reflection Coefficient) from our target impedance of Zo = 50 ohms calculates to be:
Γ = 0.8 + j0.4
And we can plot its position (using Cartesian coordinates) on the complex plane:
(click on image to enlarge)
In addition to expressing Γ's position on the complex-plane using Cartesian coordinates, we can also express its position in terms of Polar-coordinates using rho (symbol: ρ), representing the magnitude of Γ, and theta (symbol: θ), the angle it subtends from the positive x-axis.
Again using our example of the Reflection Coefficient for Zload = 50 + j200 (i.e. Γ = 0.8 + j0.4), this Γ, in Polar coordinates (rho, theta), would be:
(0.894, 26.6°)
where ρ = 0.894 and θ = 26.6 degrees:
(click on image to enlarge)
Let's plot some more Reflection Coefficients on our Complex plane. I'm going to chose eight more values for Zload, all with a resistance (i.e. "real") value of 50 ohms, and various reactance (i.e. imaginary) values, and then use Excel to calculate Γ:
(click on image to enlarge)
Here's how these eight Reflection Coefficients look when plotted on the Complex plane:
(click on image to enlarge)
If we remove the annotation from the image above, our points look like this:
(click on image to enlarge)
Looks like they form a crude circle, doesn't it?
Circles of "Constant Resistance":
If we calculate Γ for all possible Zloads of 50 ohms resistive and anything reactive, that is, Zload = 50 + jX, where X ranges from -∞ to + ∞, and we add these values to our plot of Γ above, it would become:
It's a circle! This is a circle of "constant resistance". That is, it is the locus of all possible Γ values calculated from the equation Zload = 50 + jX, where R, the resistance of Zload, is fixed at 50 ohms.
Now, if we were to calculate Γ for all possible values of Zload = R + jX, in which X ranges independently from -∞ to + ∞ and R ranges from 0 to + ∞, and then we plotted the results on the complex plane, they would plot into a region bounded by (and including) a circle of radius 1.0, centered at 0,0:
(click on image to enlarge)
Let's add a few more "constant resistance" plots of Γ to our plot of Γ for Zload = 50 + jX. I'll chose Zload = 150 + jX and Zload = 16.67 + jX, where again, X ranges from -∞ to + ∞:
(click on image to enlarge)
We have three circles, each circle representing Γ for a Zload with "constant" Resistance and all possibilities of Reactance.
Moving Along a Circle of Constant Resistance:
Lets look at what happens to our plot of Γ if we add additional series Reactance (either inductive or capacitive) to an existing value of Zload. I'll again use the example of Zload = 50 + j200.
First, let's put Γ for Zload = 50 + j200 on our "Resistance" circle:
(click on image to enlarge)
What happens if we add series reactance? We are creating a new Zload:
Zload = 50 + j200 + jX, where X is the reactance we're adding.
When we add jX to our Zload, we are going to move Γ along our "resistance" circle. The movement will be clockwise if we add inductance and counter-clockwise if we add capacitance. If we add just enough series capacitance to our "j200" term, we will cancel it out and be left with Zload = 50 + j0, a perfect match. But if we add too much capacitance, we will continue to move counter-clockwise away from that point of perfect match. To illustrate these points:
(click on image to enlarge)
We can plot the same movement for an impedance with a negative reactance. For example, consider Zload = 50- j200 ohms...
How does the value of the reactance we're adding correlate to the amount Γ moves along the circle?
We are adding a series reactance to Zload. What happens if I add a series-element that is a short circuit (zero ohms)? Nothing happens -- Γ doesn't move (that is, the impedance at that point doesn't change). So if I add a series element that has a very small reactance, that is, it looks almost a short circuit (such as a large capacitor or a small inductor), there should be little movement along the circle.
In contrast, the more the series element looks like an open-circuit (that is, the higher its reactance, e.g. small capacitor or large inductor), the greater will be Γ's movement around the circle.
(Also note that in the plot above, Γ at its limit (when jX is either -j∞ or +j∞) is at coordinate 1,0, on the circumference of the unit-circle.)
Plotting Admittance in lieu of Impedance:
But suppose we add reactance in parallel with Zload, rather than in series as was done above? How do we visually represent this?
First, recognize that any representation of Zload impedance in series form (i.e. R + jX, where R is resistance and X is reactance) can be transformed into an equivalent parallel form in which:
Yload = G + jB
Where Y is Admittance, G is Conductance, and B is Susceptance.
Yload is simply 1/Zload. Therefore, G and B can be easily calculated by inverting the equation for Zload (Zload = R + jX) which results in these two equations:
G = R/(R2 + X2), and
B = -X/(R2 + X2)
Let's calculate the equivalent Yload admittances for our example of nine impedances (all with R = 50 ohms) and add them to the table that's earlier in this post:
(click on image to enlarge)
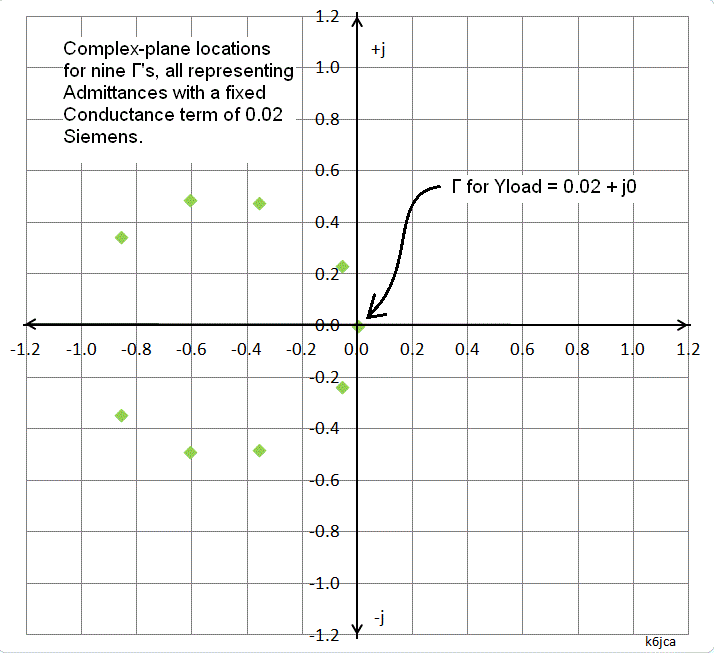
The first thing you should note: although R = 50 for all nine values, G is not constant. But take a look at G when Zload = 50 + j0 (our ideal match). It's equal to 0.02 Siemens.
So...what happens to Γ if, say, we hold Yload's Conductance (G) constant but vary Yload's Susceptance (B)?
As an example, what happens if we fix G at 0.02 Siemens? Let's calculate Γ for nine different Yloads, each with its G term set to 0.02 Siemens:
(click on image to enlarge)
Plotted on the complex plane, the coordinates for these 9 Γ are:
(click on image to enlarge)
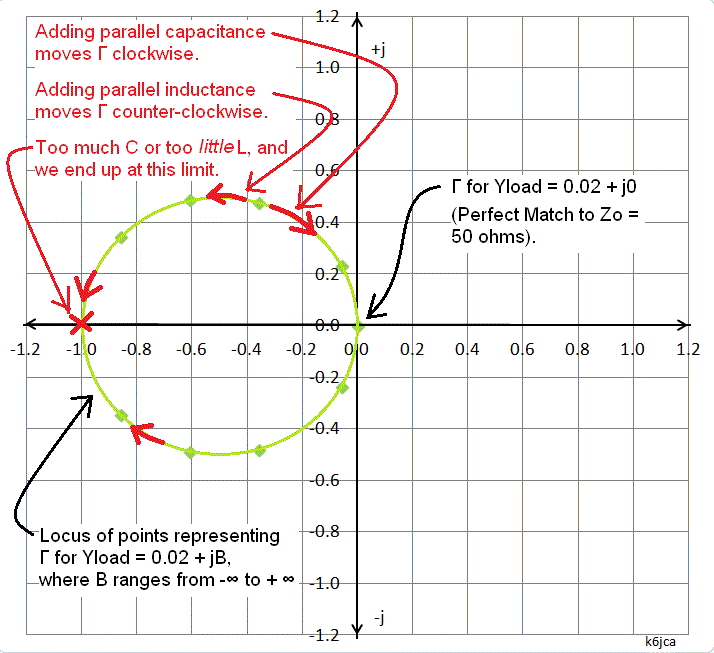
Now, again with G fixed at 0.02 Siemens, let's plot Γ for Yload = 0.02 + jB, where B ranges from -∞ to + ∞:
(click on image to enlarge)
This is a circle of "constant conductance" (in this case, G = 0.02). Note that it looks exactly like the circle of "constant resistance" that we drew above for Zload = 50 + jX, except this new circle is shifted to the left-hand side of the complex-plane.
Moving Along a Circle of Constant Conductance:
Adding either inductance or capacitance in parallel with Zload moves us along this circle. Adding inductance will move us counter-clockwise and adding capacitance moves us clockwise.
(click on image to enlarge)
How does the value of the reactance we're adding correlate to the amount Γ moves along the circle? We are adding a parallel reactance across Zload. What happens if I add a parallel-element across Zload that is an open circuit (infinite ohms)? Nothing happens -- Γ doesn't move (that is, the impedance at that point doesn't change). So if I add a parallel element that has a very large reactance, that is, it looks almost an open circuit (such as a small capacitor or a large inductor), there should be little movement along the circle.
In contrast, the more the parallel element looks like a short-circuit (that is, the lower its reactance, e.g. large capacitor or small inductor), the greater will be Γ's movement around the circle.
(Also note that in the plot above, Γ at its limit (when jB is either -j∞ or +j∞) is at coordinate -1,0, on the circumference of the unit-circle.)
For the sake of symmetry (because we did it above for circles of "constant-resistance"), let's add two more "constant-conductance" circles to the one above:
(click on image to enlarge)
And let's add our previous Γ plots of circles of constant-resistance:
(click on image to enlarge)
Arcs of Constant Reactance and of Constant Susceptance:
In addition to Γ plots of circles of constant-resistance or circles of constant-conductance, I could also plot Γwith Zload's reactance term (X) held constant and varying R from -∞ to + ∞, or I could plot Γwith Yload's susceptance term (B) held constant and varying G from -∞ to + ∞). The resulting curves would not be circles, though. Let's look at them:
Here are plots of Γ in the complex-plane with R held constant (circles) and with X held constant (arcs of circles):
(click on image to enlarge)
We have already discussed the circles of constant-resistance. The additional non-circle curves are actually arcs of circles, and they represent the segments of constant-reactance (or constant-susceptance when using admittance) circles that lie within the Smith Chart's underlying "unit circle".
We can plot these arcs by holding X constant and varying R from 0 to infinity (or, for admittance, by holding B constant and varying G from 0 to infinity).
For example, here's a plot showing the Reflection Coefficient (Gamma) for five different impedances, all of which have +200 ohms as their reactance:
If I were to plot all of the impedance which have X = +200 ohms, I would get the following arc of a circle:
(Note that the circle of "constant reactance," above, extends beyond the Smith Chart boundary. The impedances represented by the reflection-coefficients beyond the unit circle have negative resistances. For example, an impedance of -200 + j200 ohms would have a reflection coefficient equal to 1.24 + j0.32.)
With the addition of the "constant-reactance" curves, I can easily plot
Γ for any Zload = R + jX. (This is made even easier with
Smith-charting programs such as
Smith V3.10, which I
will use throughout this blog post).
For example, let's plot Γ for an impedance of Zload = 25 + j25:
I can plot the same point in terms of admittance:
And here are the admittance and impedance charts, combined:
The point represents a unique Γ, but the load associated with it can be represented either as an impedance (Z=R+jX) or as an admittance (Y=G+jB). The two forms are equivalent. But now, to move along circles of constant conductance, you would add capacitance or inductance in parallel, not in series as we did when moving along circles of constant resistance.
This is an important point, because, using the Smith Chart, we can see how adding inductance and/or capacitance in series and/or in parallel can move us from any point within the Smith Chart to its center.
Matching an Impedance to Zo:
Here's an example of how first paralleling a load with an inductance (moving along a line of constant conductance) and then adding another inductance in series to this combination (moving along a line of constant resistance) can result in a perfect match to Zo:
(More on matching here: http://k6jca.blogspot.com/2015/03/notes-on-antenna-tuners-l-network-and.html)
Smith Chart Summary:
Thus, any impedance with a positive resistance from 0 to infinite ohms and a reactance from minus-infinity to plus-infinity ohms, when converted to a reflection coefficient, can be represented by a point within the bounds of the unit-circle.
And the same holds true for any admittance. As long as the conductance is positive, any admittance, when converted to a reflection coefficient, can be represented by a point within the unit circle.
How is this useful?
First, rather than plotting impedances (or admittances) that could span to infinity on a grid (possibly a very large grid), we can plot them within a unit circle using a Smith Chart.
In a similar vein, we could also plot other data related to these impedances. Here's an example of antenna tuner loss of a lowpass L Network (when tuned to a match), plotted against the tuner's load impedance. The load impedance is defined by the Smith Chart's co-ordinates, and the loss is calculated assuming the Q's of 100 for the L-network's inductor and capacitor.
(Go here for more info: http://k6jca.blogspot.com/2018/09/plotting-3-d-smith-charts-with-matlab.html)
Second, a Vector Network Analyzer (VNA) actually measures a network's Reflection Coefficient (its S11 or S22 measurements). The Smith Chart lets us translate the VNA's measured co-ordinates of a Reflection Coefficient point (expressed as either Cartesian or Polar coordinates) into an impedance.
That is, we can consider the Smith Chart to be an "overlay" which we could place over a plot of Reflection Coefficients, and, using this overlay, we could determine the impedance represented by each point of the Reflection Coefficient plot.
In fact, early Vector Network Analyzers did just this -- for example Hewlett Packard supplied the user with various transparent overlays that would fit over their 8505A VNA's CRT, and one of these overlays was a Smith Chart overlay. Here's the cover from the July, 1976 issue of the Hewlett-Packard Journal -- the cover's background is the CRT of HP's 8505A Vector Network Analyzer with the Smith Chart overlay mounted in front of it.
One important point about the image, above.
If you look at the Smith Chart overlay, you will see that its center is labeled as 1.0, rather than the 50 ohms that I've been using in this blog post. There is nothing strange in this, and you will come across it quite often. In this situation, the reflection coefficient's equation has been "normalized" by dividing both its numerator and denominator by Zo. That is, rather than representing the Reflection Coefficient as being calculated by:
Γ = (Zload - Zo) / (Zload + Zo),
the equation is transformed to be:
Γ = (Zload/Zo - 1) / (Zload/Zo + 1),
Note that the two equations are equivalent. But now, rather than representing R + jX, the Smith Chart's circles and arcs represent R/Zo + jX/Zo. (Ditto for admittances)
And so in this case, the center of the unit circle, rather than being labeled "50" (i.e. Zo for my examples), is labeled "1" (i.e. 50/Zo).
Why do this? It allows a common Smith Chart (for example, the 8505A's overlay) to be used with non-50 ohms systems (e.g. a 75 ohms system).
Circles of Constant SWR:
One more quick topic: circles of constant SWR.
SWR can be calculated from Γ:
(Note: some authors use ρ in lieu of Γ to represent the
Reflection Coefficient. I believe it less confusing to represent the
Reflection Coefficient with Γ and its magnitude with ρ).
The SWR for any ρ (that is, |Γ|) can be plotted as an overlay on the Smith Chart. For any given ρ, the set of impedance (or admittances) that result in this ρ will lie on a circle centered at (0,0) and with radius ρ. Here are some examples:
That's it for the tutorial. To recap, the important points are these:
Resources:
You can download the Smith-chart software here: Smith V3.10
Other sites you might want to visit:
http://www.antenna-theory.com/tutorial/smith/chart.php
http://www.antenna-theory.com/tutorial/txline/transmissionline.php
Antenna Tuner Blog Posts:
A quick tutorial on Smith Chart basics:
http://k6jca.blogspot.com/2015/03/a-brief-tutorial-on-smith-charts.html
Plotting Smith Chart Data in 3-D:
http://k6jca.blogspot.com/2018/09/plotting-3-d-smith-charts-with-matlab.html
The L-network:
http://k6jca.blogspot.com/2015/03/notes-on-antenna-tuners-l-network-and.html
A correction to the usual L-network design constraints:
http://k6jca.blogspot.com/2015/04/revisiting-l-network-equations-and.html
Calculating L-Network values when the components are lossy:
http://k6jca.blogspot.com/2018/09/l-networks-new-equations-for-better.html
A look at highpass T-Networks:
http://k6jca.blogspot.com/2015/04/notes-on-antenna-tuners-t-network-part-1.html
More on the W8ZR EZ-Tuner:
http://k6jca.blogspot.com/2015/05/notes-on-antenna-tuners-more-on-w8zr-ez.html (Note that this tuner is also discussed in the highpass T-Network post).
The Elecraft KAT-500:
http://k6jca.blogspot.com/2015/05/notes-on-antenna-tuners-elecraft-kat500.html
The Nye Viking MB-V-A tuner and the Rohde Coupler:
http://k6jca.blogspot.com/2015/05/notes-on-antenna-tuners-nye-viking-mb-v.html
The Drake MN-4 Tuner:
http://k6jca.blogspot.com/2018/08/notes-on-antenna-tuners-drake-mn-4.html
Thanks
Many thanks to Jerry Gaffke, KE7ER, for his recommendations.
Caveats:
I could have easily made a mistake anywhere in this blog post. If something looks wrong, is unclear, or doesn't make sense, please feel free to contact me!
For example, let's plot Γ for an impedance of Zload = 25 + j25:
(click on image to enlarge)
I can plot the same point in terms of admittance:
(click on image to enlarge)
And here are the admittance and impedance charts, combined:
(click on image to enlarge)
The point represents a unique Γ, but the load associated with it can be represented either as an impedance (Z=R+jX) or as an admittance (Y=G+jB). The two forms are equivalent. But now, to move along circles of constant conductance, you would add capacitance or inductance in parallel, not in series as we did when moving along circles of constant resistance.
This is an important point, because, using the Smith Chart, we can see how adding inductance and/or capacitance in series and/or in parallel can move us from any point within the Smith Chart to its center.
Matching an Impedance to Zo:
Here's an example of how first paralleling a load with an inductance (moving along a line of constant conductance) and then adding another inductance in series to this combination (moving along a line of constant resistance) can result in a perfect match to Zo:
(More on matching here: http://k6jca.blogspot.com/2015/03/notes-on-antenna-tuners-l-network-and.html)
Smith Chart Summary:
Thus, any impedance with a positive resistance from 0 to infinite ohms and a reactance from minus-infinity to plus-infinity ohms, when converted to a reflection coefficient, can be represented by a point within the bounds of the unit-circle.
And the same holds true for any admittance. As long as the conductance is positive, any admittance, when converted to a reflection coefficient, can be represented by a point within the unit circle.
How is this useful?
First, rather than plotting impedances (or admittances) that could span to infinity on a grid (possibly a very large grid), we can plot them within a unit circle using a Smith Chart.
In a similar vein, we could also plot other data related to these impedances. Here's an example of antenna tuner loss of a lowpass L Network (when tuned to a match), plotted against the tuner's load impedance. The load impedance is defined by the Smith Chart's co-ordinates, and the loss is calculated assuming the Q's of 100 for the L-network's inductor and capacitor.
(Go here for more info: http://k6jca.blogspot.com/2018/09/plotting-3-d-smith-charts-with-matlab.html)
Second, a Vector Network Analyzer (VNA) actually measures a network's Reflection Coefficient (its S11 or S22 measurements). The Smith Chart lets us translate the VNA's measured co-ordinates of a Reflection Coefficient point (expressed as either Cartesian or Polar coordinates) into an impedance.
That is, we can consider the Smith Chart to be an "overlay" which we could place over a plot of Reflection Coefficients, and, using this overlay, we could determine the impedance represented by each point of the Reflection Coefficient plot.
In fact, early Vector Network Analyzers did just this -- for example Hewlett Packard supplied the user with various transparent overlays that would fit over their 8505A VNA's CRT, and one of these overlays was a Smith Chart overlay. Here's the cover from the July, 1976 issue of the Hewlett-Packard Journal -- the cover's background is the CRT of HP's 8505A Vector Network Analyzer with the Smith Chart overlay mounted in front of it.
One important point about the image, above.
If you look at the Smith Chart overlay, you will see that its center is labeled as 1.0, rather than the 50 ohms that I've been using in this blog post. There is nothing strange in this, and you will come across it quite often. In this situation, the reflection coefficient's equation has been "normalized" by dividing both its numerator and denominator by Zo. That is, rather than representing the Reflection Coefficient as being calculated by:
Γ = (Zload - Zo) / (Zload + Zo),
the equation is transformed to be:
Γ = (Zload/Zo - 1) / (Zload/Zo + 1),
Note that the two equations are equivalent. But now, rather than representing R + jX, the Smith Chart's circles and arcs represent R/Zo + jX/Zo. (Ditto for admittances)
And so in this case, the center of the unit circle, rather than being labeled "50" (i.e. Zo for my examples), is labeled "1" (i.e. 50/Zo).
Why do this? It allows a common Smith Chart (for example, the 8505A's overlay) to be used with non-50 ohms systems (e.g. a 75 ohms system).
Circles of Constant SWR:
One more quick topic: circles of constant SWR.
SWR can be calculated from Γ:
SWR = (1 + |Γ|) / (1 - |Γ|)
That is, SWR depends on the magnitude of Γ. But the magnitude
of Γ is also rho, ρ (see discussion at the beginning of this
post). And so we could also write the equation in terms of ρ:
SWR = (1 + ρ) / (1 - ρ)
The SWR for any ρ (that is, |Γ|) can be plotted as an overlay on the Smith Chart. For any given ρ, the set of impedance (or admittances) that result in this ρ will lie on a circle centered at (0,0) and with radius ρ. Here are some examples:
(click on image to enlarge)
That's it for the tutorial. To recap, the important points are these:
First, a load's Reflection Coefficient (Γ) can be plotted on the complex-plane. This plotted point will have a magnitude (also known as ρ), when referenced to the center of the plane (0,0), that is between (and inclusive of) 0 and 1.
Second, the Smith Chart itself is simply an overlay over this plot of the Reflection Coefficient, and this overlay identifies the impedance (or admittance) of the load associated with Γ at any point. This plot could be in terms of a specific Zo (e.g. 50 ohms) or Zo might be normalized to 1.
Third, if we add capacitance or inductance in series with our load we can visualize this as moving Γ along Smith Chart circles of constant-resistance (the direction will depend on the sign of the reactance: inductive or capacitive). And in an analogous fashion, if we add capacitance or inductance in parallel with our load, we will move Γ along circles of constant-conductance.
Fourth, when we add capacitance or inductance to our circuit, this movement of Γ (and thus the change in impedance or admittance) is only along these circles. It is not along the other lines representing constant-reactance or constant susceptance.
Fifth, circles of constant SWR can be plotted on the Smith Chart. These circles are centered at (0,0) -- the chart's Zo, and their radius is a function of ρ, the magnitude of Γ.I'll note, too, that the Smith Chart has other uses beyond those discussed above, and I would recommend the interested reader to explore further.
Resources:
You can download the Smith-chart software here: Smith V3.10
Other sites you might want to visit:
http://www.antenna-theory.com/tutorial/smith/chart.php
http://www.antenna-theory.com/tutorial/txline/transmissionline.php
Antenna Tuner Blog Posts:
A quick tutorial on Smith Chart basics:
http://k6jca.blogspot.com/2015/03/a-brief-tutorial-on-smith-charts.html
Plotting Smith Chart Data in 3-D:
http://k6jca.blogspot.com/2018/09/plotting-3-d-smith-charts-with-matlab.html
The L-network:
http://k6jca.blogspot.com/2015/03/notes-on-antenna-tuners-l-network-and.html
A correction to the usual L-network design constraints:
http://k6jca.blogspot.com/2015/04/revisiting-l-network-equations-and.html
Calculating L-Network values when the components are lossy:
http://k6jca.blogspot.com/2018/09/l-networks-new-equations-for-better.html
A look at highpass T-Networks:
http://k6jca.blogspot.com/2015/04/notes-on-antenna-tuners-t-network-part-1.html
More on the W8ZR EZ-Tuner:
http://k6jca.blogspot.com/2015/05/notes-on-antenna-tuners-more-on-w8zr-ez.html (Note that this tuner is also discussed in the highpass T-Network post).
The Elecraft KAT-500:
http://k6jca.blogspot.com/2015/05/notes-on-antenna-tuners-elecraft-kat500.html
The Nye Viking MB-V-A tuner and the Rohde Coupler:
http://k6jca.blogspot.com/2015/05/notes-on-antenna-tuners-nye-viking-mb-v.html
http://k6jca.blogspot.com/2018/08/notes-on-antenna-tuners-drake-mn-4.html
Measuring a Tuner's "Match-Space":
Measuring Tuner Power Loss:
Thanks
Many thanks to Jerry Gaffke, KE7ER, for his recommendations.
Caveats:
I could have easily made a mistake anywhere in this blog post. If something looks wrong, is unclear, or doesn't make sense, please feel free to contact me!










































3 comments:
This was an exceptionally good explanation. Thank you.
Good job👌👌👌
Super artykuł !
Post a Comment