This blog post presents a new set of design equations for low-pass L-network configurations that include component losses. The resulting calculated L and C component values will provide the correct impedance transformation, irrespective of component Q.
And this post will show how MATLAB's Symbolic Math Toolbox is used to generate these equations (thanks to Dick Benson, W1QG).
Important Note: The equations will be for the LsCp and CpLs low-pass L-Network configurations, shown in the schematics, below. Design equations for other network configurations can be derived in a similar fashion to the derivation process I will present later in this post.
Example, Calculating L-Network Values without Loss:
First, let's look at calculating L-network values for an LsCp network and for a CpLs network, assuming the components are lossless (i.e. infinite Q).
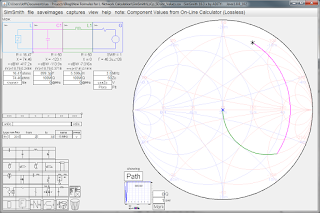
First, let me pick some load impedances. As Zload (the load impedance), I'll choose two points from the outer edge of the plot below from my earlier L-network post (note that this edge corresponds to a 10:1 SWR circle, and that the Smith Chart below happens to be displaying power-loss for a lossy matching network).
I'm going to choose the two points where, if component Qs were 100, the L-network would experience its worst power dissipation. These two points are at 66 and 246 degrees:
- At 66 degrees Zload is 16.47 + j74.46 ohms.
- At 246 degrees Zload is 7.079 - j32.01 ohms.
Let's use an on-line calculator, Impedance Matching Network Designer, to find the L-network component values for each load. Note that the calculator assumes that the L and C components are lossless (i.e. component Q is infinite).
For Zload = 7.079 - j32.01 ohms at 3.5 MHz, the on-line calculator returns the following component values:
Note that the matching network is a CpLs L-network configuration.
And for Zload = 7.079 - j32.01 ohms at 3.5 MHz, the on-line calculator returns the following component values:
This load requires an LsCp L-network configuration.
Let's now plot the resulting matches on Smith Charts to check that they indeed provide a match. Component Qs are set to be essentially infinite.
First, the CpLs network:
And now the LsCp network:
Both networks match to a 1:1 SWR.
But suppose the network components are instead lossy (i.e. finite Qs), rather than lossless? Let's see what happens to the SWR if I change the inductor Q and the capacitor Q to each equal 100. Below are the new Smith Charts...
The CpLs network:
And the LsCp network:
In these two examples the calculated L-network values no longer provide a 1:1 match! And if component Qs were to decrease further (so that there is more loss), the match would worsen.
Clearly this is not our goal. Is there a way to accurately calculate L and C component values that take into account real-world component loss?
Yes there is! Let's look at a set of equations that will exactly calculate the requisite L-network component values to provide a 1:1 match even if these components have low Q values. And we can derive the equations that do this using MATLAB's Symbolic Math Toolbox.
Example, Calculating L-Network Values with Loss:
Before delving into the equations themselves and their derivation, let me first calculate the component values using these new equations and show that the values, with finite Q (in this case, 100), provide a 1:1 match.
For a CpLs network, the MATLAB script calculates and returns two pairs of inductive (XL) and capacitive (XC) reactance values, given Zload, component Qs, and Zsource. If a CpLs network exists for this load, then one of the XL,XC pairs will have both of its values positive and real (no imaginary component). Pairs in which either (or both) values is negative or complex means that the pair is invalid.
Below I've shown the valid XL, XC pair required for the CpLs network to match a Zload of 16.47 + j74.46 ohms, given an inductor Q of 100 and a capacitor Q of 100.
And below is a similar calculation for a Zload of 7.079 - j32.01 ohms and the same network component Qs. This time, I've calculated the values for an LsCp network. And again, only one pair of values meets the "both positive and real" criteria.
Given these XL and XC values and an operating frequency of 3.5 MHz, we can easily calculate the capacitance and inductance values from these reactances (an exercise left to the reader, but you will see that I've inserted these values into the SimSmith charts, below).
And here are the resultant Smith Charts. You can see that the resulting SWRs are now 1:1, even with finite component Qs.
Here is a table with a comparison of the SWRs for the on-line calculator values versus the values found via MATLAB's Symbolic Math:
Note the higher SWR when the Q of the components calculated with the on-line calculator are each 100, compared to the components calculated with MATLAB.
What are the new equations and how were they derived? Let's look at the MATLAB scripts:
The MATLAB Scripts:
Below is the MATLAB script to calculate the XL and XC values for a CpLs low-pass L-network. Note that its inputs are Zload, Zsource, Qinductor and Qcapacitor. The outputs are Xinductor and Xcapacitor. These are seriously complex equations!
function [ X_L_Val, X_C_Val ] = shunt_C_ser_L_Q_3(Rload,Xload,Rsource,Xsource,Q_L,Q_C) close clc % Formulas generated using symbolic math % generated in the script: SymMath_CpLs_from_Qs_and_Zload_3.m % This third version calculates X_C in lieu of B_C % First, calculating the two XL values: X_L_Val(1) = (Q_L*(Q_C*Rsource^2 - 2*Rload*Xsource + Q_L*Rsource^2 + Q_C*Xsource^2 + Q_L*Xsource^2 + (- 4*Q_C^2*Q_L^2*Rload^2*Rsource^2 + 4*Q_C^2*Q_L^2*Rload*Rsource^3 + 4*Q_C^2*Q_L^2*Rload*Rsource*Xsource^2 + 8*Q_C^2*Q_L*Rload*Rsource^2*Xload - 4*Q_C^2*Q_L*Rsource^3*Xload - 4*Q_C^2*Q_L*Rsource*Xload*Xsource^2 + Q_C^2*Rsource^4 - 4*Q_C^2*Rsource^2*Xload^2 + 2*Q_C^2*Rsource^2*Xsource^2 + Q_C^2*Xsource^4 - 8*Q_C*Q_L^2*Rload^2*Rsource*Xsource + 4*Q_C*Q_L^2*Rload*Rsource^2*Xsource + 4*Q_C*Q_L^2*Rload*Xsource^3 - 4*Q_C*Q_L*Rload*Rsource^3 + 16*Q_C*Q_L*Rload*Rsource*Xload*Xsource - 4*Q_C*Q_L*Rload*Rsource*Xsource^2 + 2*Q_C*Q_L*Rsource^4 - 4*Q_C*Q_L*Rsource^2*Xload*Xsource + 4*Q_C*Q_L*Rsource^2*Xsource^2 - 4*Q_C*Q_L*Xload*Xsource^3 + 2*Q_C*Q_L*Xsource^4 + 4*Q_C*Rsource^3*Xload - 8*Q_C*Rsource*Xload^2*Xsource + 4*Q_C*Rsource*Xload*Xsource^2 - 4*Q_L^2*Rload^2*Xsource^2 + Q_L^2*Rsource^4 + 2*Q_L^2*Rsource^2*Xsource^2 + Q_L^2*Xsource^4 - 4*Q_L*Rload*Rsource^2*Xsource + 8*Q_L*Rload*Xload*Xsource^2 - 4*Q_L*Rload*Xsource^3 + 4*Rsource^2*Xload*Xsource - 4*Xload^2*Xsource^2 + 4*Xload*Xsource^3)^(1/2) - 2*Q_C*Rload*Rsource - 2*Q_L*Xload*Xsource - 2*Q_C*Q_L*Rsource*Xload))/(2*(Q_L^2 + 1)*(Xsource + Q_C*Rsource)); X_L_Val(2) = -(Q_L*(2*Rload*Xsource - Q_C*Rsource^2 - Q_L*Rsource^2 - Q_C*Xsource^2 - Q_L*Xsource^2 + (- 4*Q_C^2*Q_L^2*Rload^2*Rsource^2 + 4*Q_C^2*Q_L^2*Rload*Rsource^3 + 4*Q_C^2*Q_L^2*Rload*Rsource*Xsource^2 + 8*Q_C^2*Q_L*Rload*Rsource^2*Xload - 4*Q_C^2*Q_L*Rsource^3*Xload - 4*Q_C^2*Q_L*Rsource*Xload*Xsource^2 + Q_C^2*Rsource^4 - 4*Q_C^2*Rsource^2*Xload^2 + 2*Q_C^2*Rsource^2*Xsource^2 + Q_C^2*Xsource^4 - 8*Q_C*Q_L^2*Rload^2*Rsource*Xsource + 4*Q_C*Q_L^2*Rload*Rsource^2*Xsource + 4*Q_C*Q_L^2*Rload*Xsource^3 - 4*Q_C*Q_L*Rload*Rsource^3 + 16*Q_C*Q_L*Rload*Rsource*Xload*Xsource - 4*Q_C*Q_L*Rload*Rsource*Xsource^2 + 2*Q_C*Q_L*Rsource^4 - 4*Q_C*Q_L*Rsource^2*Xload*Xsource + 4*Q_C*Q_L*Rsource^2*Xsource^2 - 4*Q_C*Q_L*Xload*Xsource^3 + 2*Q_C*Q_L*Xsource^4 + 4*Q_C*Rsource^3*Xload - 8*Q_C*Rsource*Xload^2*Xsource + 4*Q_C*Rsource*Xload*Xsource^2 - 4*Q_L^2*Rload^2*Xsource^2 + Q_L^2*Rsource^4 + 2*Q_L^2*Rsource^2*Xsource^2 + Q_L^2*Xsource^4 - 4*Q_L*Rload*Rsource^2*Xsource + 8*Q_L*Rload*Xload*Xsource^2 - 4*Q_L*Rload*Xsource^3 + 4*Rsource^2*Xload*Xsource - 4*Xload^2*Xsource^2 + 4*Xload*Xsource^3)^(1/2) + 2*Q_C*Rload*Rsource + 2*Q_L*Xload*Xsource + 2*Q_C*Q_L*Rsource*Xload))/(2*(Q_L^2 + 1)*(Xsource + Q_C*Rsource)); % ...and calculate the two XC values: X_C_Val(1) = (Q_C*(2*Rsource*Xload + Q_C*Rsource^2 + Q_L*Rsource^2 + Q_C*Xsource^2 + Q_L*Xsource^2 + (- 4*Q_C^2*Q_L^2*Rload^2*Rsource^2 + 4*Q_C^2*Q_L^2*Rload*Rsource^3 + 4*Q_C^2*Q_L^2*Rload*Rsource*Xsource^2 + 8*Q_C^2*Q_L*Rload*Rsource^2*Xload - 4*Q_C^2*Q_L*Rsource^3*Xload - 4*Q_C^2*Q_L*Rsource*Xload*Xsource^2 + Q_C^2*Rsource^4 - 4*Q_C^2*Rsource^2*Xload^2 + 2*Q_C^2*Rsource^2*Xsource^2 + Q_C^2*Xsource^4 - 8*Q_C*Q_L^2*Rload^2*Rsource*Xsource + 4*Q_C*Q_L^2*Rload*Rsource^2*Xsource + 4*Q_C*Q_L^2*Rload*Xsource^3 - 4*Q_C*Q_L*Rload*Rsource^3 + 16*Q_C*Q_L*Rload*Rsource*Xload*Xsource - 4*Q_C*Q_L*Rload*Rsource*Xsource^2 + 2*Q_C*Q_L*Rsource^4 - 4*Q_C*Q_L*Rsource^2*Xload*Xsource + 4*Q_C*Q_L*Rsource^2*Xsource^2 - 4*Q_C*Q_L*Xload*Xsource^3 + 2*Q_C*Q_L*Xsource^4 + 4*Q_C*Rsource^3*Xload - 8*Q_C*Rsource*Xload^2*Xsource + 4*Q_C*Rsource*Xload*Xsource^2 - 4*Q_L^2*Rload^2*Xsource^2 + Q_L^2*Rsource^4 + 2*Q_L^2*Rsource^2*Xsource^2 + Q_L^2*Xsource^4 - 4*Q_L*Rload*Rsource^2*Xsource + 8*Q_L*Rload*Xload*Xsource^2 - 4*Q_L*Rload*Xsource^3 + 4*Rsource^2*Xload*Xsource - 4*Xload^2*Xsource^2 + 4*Xload*Xsource^3)^(1/2) - 2*Q_L*Rload*Rsource - 2*Q_C*Xload*Xsource + 2*Q_C*Q_L*Rload*Xsource))/(2*(Q_C^2 + 1)*(Xload - Xsource - Q_L*Rload + Q_L*Rsource)); X_C_Val(2) = (Q_C*(2*Rsource*Xload + Q_C*Rsource^2 + Q_L*Rsource^2 + Q_C*Xsource^2 + Q_L*Xsource^2 - (- 4*Q_C^2*Q_L^2*Rload^2*Rsource^2 + 4*Q_C^2*Q_L^2*Rload*Rsource^3 + 4*Q_C^2*Q_L^2*Rload*Rsource*Xsource^2 + 8*Q_C^2*Q_L*Rload*Rsource^2*Xload - 4*Q_C^2*Q_L*Rsource^3*Xload - 4*Q_C^2*Q_L*Rsource*Xload*Xsource^2 + Q_C^2*Rsource^4 - 4*Q_C^2*Rsource^2*Xload^2 + 2*Q_C^2*Rsource^2*Xsource^2 + Q_C^2*Xsource^4 - 8*Q_C*Q_L^2*Rload^2*Rsource*Xsource + 4*Q_C*Q_L^2*Rload*Rsource^2*Xsource + 4*Q_C*Q_L^2*Rload*Xsource^3 - 4*Q_C*Q_L*Rload*Rsource^3 + 16*Q_C*Q_L*Rload*Rsource*Xload*Xsource - 4*Q_C*Q_L*Rload*Rsource*Xsource^2 + 2*Q_C*Q_L*Rsource^4 - 4*Q_C*Q_L*Rsource^2*Xload*Xsource + 4*Q_C*Q_L*Rsource^2*Xsource^2 - 4*Q_C*Q_L*Xload*Xsource^3 + 2*Q_C*Q_L*Xsource^4 + 4*Q_C*Rsource^3*Xload - 8*Q_C*Rsource*Xload^2*Xsource + 4*Q_C*Rsource*Xload*Xsource^2 - 4*Q_L^2*Rload^2*Xsource^2 + Q_L^2*Rsource^4 + 2*Q_L^2*Rsource^2*Xsource^2 + Q_L^2*Xsource^4 - 4*Q_L*Rload*Rsource^2*Xsource + 8*Q_L*Rload*Xload*Xsource^2 - 4*Q_L*Rload*Xsource^3 + 4*Rsource^2*Xload*Xsource - 4*Xload^2*Xsource^2 + 4*Xload*Xsource^3)^(1/2) - 2*Q_L*Rload*Rsource - 2*Q_C*Xload*Xsource + 2*Q_C*Q_L*Rload*Xsource))/(2*(Q_C^2 + 1)*(Xload - Xsource - Q_L*Rload + Q_L*Rsource)); end
(Published with MATLAB® R2018a)
And below is the MATLAB script (written in large part by Dick Benson, W1QG), using the Symbolic Math Toolbox, that created the four equations, above:
% Script Name: SymMath_CpLs_from_Qs_and_Zload_3.m % SYMBOLIC Analysis .... work from Source to Load to get Zin % Source, Series L then Shunt C , then load % k6jca: modified w1qg's code, and now use X_C in lieu of B_C % Make sure the 'syms' line, below is terminated with "real"! syms Rsource Xsource Rload Xload X_L Q_L X_C Q_C real Zseries = (X_L/Q_L + Rload) + 1i*(X_L + Xload); % Rs = Xs/Q Zshunt = (X_C/Q_C) - (1i*X_C); % Rs = Xs/Q Zin = 1/(1/Zshunt + 1/Zseries); eq1 = simplify(real(Zin),'Criterion','preferReal','Steps',50); eq2 = simplify(imag(Zin),'Criterion','preferReal','Steps',50); [X_L_Sol, X_C_Sol] = solve([eq1==Rsource,eq2==Xsource],[X_L,X_C]); XLS= simplify(X_L_Sol,'Steps',50) XCS= simplify(X_C_Sol,'Steps',50) % The resulting four equations will appear in MATLAB's % Command Window, from which they are copied and pasted into % the script: shunt_C_ser_L_Q_3.mXLS = (Q_L*(Q_C*Rsource^2 - 2*Rload*Xsource + Q_L*Rsource^2 + Q_C*Xsource^2 + Q_L*Xsource^2 + (- 4*Q_C^2*Q_L^2*Rload^2*Rsource^2 + 4*Q_C^2*Q_L^2*Rload*Rsource^3 + 4*Q_C^2*Q_L^2*Rload*Rsource*Xsource^2 + 8*Q_C^2*Q_L*Rload*Rsource^2*Xload - 4*Q_C^2*Q_L*Rsource^3*Xload - 4*Q_C^2*Q_L*Rsource*Xload*Xsource^2 + Q_C^2*Rsource^4 - 4*Q_C^2*Rsource^2*Xload^2 + 2*Q_C^2*Rsource^2*Xsource^2 + Q_C^2*Xsource^4 - 8*Q_C*Q_L^2*Rload^2*Rsource*Xsource + 4*Q_C*Q_L^2*Rload*Rsource^2*Xsource + 4*Q_C*Q_L^2*Rload*Xsource^3 - 4*Q_C*Q_L*Rload*Rsource^3 + 16*Q_C*Q_L*Rload*Rsource*Xload*Xsource - 4*Q_C*Q_L*Rload*Rsource*Xsource^2 + 2*Q_C*Q_L*Rsource^4 - 4*Q_C*Q_L*Rsource^2*Xload*Xsource + 4*Q_C*Q_L*Rsource^2*Xsource^2 - 4*Q_C*Q_L*Xload*Xsource^3 + 2*Q_C*Q_L*Xsource^4 + 4*Q_C*Rsource^3*Xload - 8*Q_C*Rsource*Xload^2*Xsource + 4*Q_C*Rsource*Xload*Xsource^2 - 4*Q_L^2*Rload^2*Xsource^2 + Q_L^2*Rsource^4 + 2*Q_L^2*Rsource^2*Xsource^2 + Q_L^2*Xsource^4 - 4*Q_L*Rload*Rsource^2*Xsource + 8*Q_L*Rload*Xload*Xsource^2 - 4*Q_L*Rload*Xsource^3 + 4*Rsource^2*Xload*Xsource - 4*Xload^2*Xsource^2 + 4*Xload*Xsource^3)^(1/2) - 2*Q_C*Rload*Rsource - 2*Q_L*Xload*Xsource - 2*Q_C*Q_L*Rsource*Xload))/(2*(Q_L^2 + 1)*(Xsource + Q_C*Rsource)) -(Q_L*(2*Rload*Xsource - Q_C*Rsource^2 - Q_L*Rsource^2 - Q_C*Xsource^2 - Q_L*Xsource^2 + (- 4*Q_C^2*Q_L^2*Rload^2*Rsource^2 + 4*Q_C^2*Q_L^2*Rload*Rsource^3 + 4*Q_C^2*Q_L^2*Rload*Rsource*Xsource^2 + 8*Q_C^2*Q_L*Rload*Rsource^2*Xload - 4*Q_C^2*Q_L*Rsource^3*Xload - 4*Q_C^2*Q_L*Rsource*Xload*Xsource^2 + Q_C^2*Rsource^4 - 4*Q_C^2*Rsource^2*Xload^2 + 2*Q_C^2*Rsource^2*Xsource^2 + Q_C^2*Xsource^4 - 8*Q_C*Q_L^2*Rload^2*Rsource*Xsource + 4*Q_C*Q_L^2*Rload*Rsource^2*Xsource + 4*Q_C*Q_L^2*Rload*Xsource^3 - 4*Q_C*Q_L*Rload*Rsource^3 + 16*Q_C*Q_L*Rload*Rsource*Xload*Xsource - 4*Q_C*Q_L*Rload*Rsource*Xsource^2 + 2*Q_C*Q_L*Rsource^4 - 4*Q_C*Q_L*Rsource^2*Xload*Xsource + 4*Q_C*Q_L*Rsource^2*Xsource^2 - 4*Q_C*Q_L*Xload*Xsource^3 + 2*Q_C*Q_L*Xsource^4 + 4*Q_C*Rsource^3*Xload - 8*Q_C*Rsource*Xload^2*Xsource + 4*Q_C*Rsource*Xload*Xsource^2 - 4*Q_L^2*Rload^2*Xsource^2 + Q_L^2*Rsource^4 + 2*Q_L^2*Rsource^2*Xsource^2 + Q_L^2*Xsource^4 - 4*Q_L*Rload*Rsource^2*Xsource + 8*Q_L*Rload*Xload*Xsource^2 - 4*Q_L*Rload*Xsource^3 + 4*Rsource^2*Xload*Xsource - 4*Xload^2*Xsource^2 + 4*Xload*Xsource^3)^(1/2) + 2*Q_C*Rload*Rsource + 2*Q_L*Xload*Xsource + 2*Q_C*Q_L*Rsource*Xload))/(2*(Q_L^2 + 1)*(Xsource + Q_C*Rsource)) XCS = (Q_C*(2*Rsource*Xload + Q_C*Rsource^2 + Q_L*Rsource^2 + Q_C*Xsource^2 + Q_L*Xsource^2 + (- 4*Q_C^2*Q_L^2*Rload^2*Rsource^2 + 4*Q_C^2*Q_L^2*Rload*Rsource^3 + 4*Q_C^2*Q_L^2*Rload*Rsource*Xsource^2 + 8*Q_C^2*Q_L*Rload*Rsource^2*Xload - 4*Q_C^2*Q_L*Rsource^3*Xload - 4*Q_C^2*Q_L*Rsource*Xload*Xsource^2 + Q_C^2*Rsource^4 - 4*Q_C^2*Rsource^2*Xload^2 + 2*Q_C^2*Rsource^2*Xsource^2 + Q_C^2*Xsource^4 - 8*Q_C*Q_L^2*Rload^2*Rsource*Xsource + 4*Q_C*Q_L^2*Rload*Rsource^2*Xsource + 4*Q_C*Q_L^2*Rload*Xsource^3 - 4*Q_C*Q_L*Rload*Rsource^3 + 16*Q_C*Q_L*Rload*Rsource*Xload*Xsource - 4*Q_C*Q_L*Rload*Rsource*Xsource^2 + 2*Q_C*Q_L*Rsource^4 - 4*Q_C*Q_L*Rsource^2*Xload*Xsource + 4*Q_C*Q_L*Rsource^2*Xsource^2 - 4*Q_C*Q_L*Xload*Xsource^3 + 2*Q_C*Q_L*Xsource^4 + 4*Q_C*Rsource^3*Xload - 8*Q_C*Rsource*Xload^2*Xsource + 4*Q_C*Rsource*Xload*Xsource^2 - 4*Q_L^2*Rload^2*Xsource^2 + Q_L^2*Rsource^4 + 2*Q_L^2*Rsource^2*Xsource^2 + Q_L^2*Xsource^4 - 4*Q_L*Rload*Rsource^2*Xsource + 8*Q_L*Rload*Xload*Xsource^2 - 4*Q_L*Rload*Xsource^3 + 4*Rsource^2*Xload*Xsource - 4*Xload^2*Xsource^2 + 4*Xload*Xsource^3)^(1/2) - 2*Q_L*Rload*Rsource - 2*Q_C*Xload*Xsource + 2*Q_C*Q_L*Rload*Xsource))/(2*(Q_C^2 + 1)*(Xload - Xsource - Q_L*Rload + Q_L*Rsource)) (Q_C*(2*Rsource*Xload + Q_C*Rsource^2 + Q_L*Rsource^2 + Q_C*Xsource^2 + Q_L*Xsource^2 - (- 4*Q_C^2*Q_L^2*Rload^2*Rsource^2 + 4*Q_C^2*Q_L^2*Rload*Rsource^3 + 4*Q_C^2*Q_L^2*Rload*Rsource*Xsource^2 + 8*Q_C^2*Q_L*Rload*Rsource^2*Xload - 4*Q_C^2*Q_L*Rsource^3*Xload - 4*Q_C^2*Q_L*Rsource*Xload*Xsource^2 + Q_C^2*Rsource^4 - 4*Q_C^2*Rsource^2*Xload^2 + 2*Q_C^2*Rsource^2*Xsource^2 + Q_C^2*Xsource^4 - 8*Q_C*Q_L^2*Rload^2*Rsource*Xsource + 4*Q_C*Q_L^2*Rload*Rsource^2*Xsource + 4*Q_C*Q_L^2*Rload*Xsource^3 - 4*Q_C*Q_L*Rload*Rsource^3 + 16*Q_C*Q_L*Rload*Rsource*Xload*Xsource - 4*Q_C*Q_L*Rload*Rsource*Xsource^2 + 2*Q_C*Q_L*Rsource^4 - 4*Q_C*Q_L*Rsource^2*Xload*Xsource + 4*Q_C*Q_L*Rsource^2*Xsource^2 - 4*Q_C*Q_L*Xload*Xsource^3 + 2*Q_C*Q_L*Xsource^4 + 4*Q_C*Rsource^3*Xload - 8*Q_C*Rsource*Xload^2*Xsource + 4*Q_C*Rsource*Xload*Xsource^2 - 4*Q_L^2*Rload^2*Xsource^2 + Q_L^2*Rsource^4 + 2*Q_L^2*Rsource^2*Xsource^2 + Q_L^2*Xsource^4 - 4*Q_L*Rload*Rsource^2*Xsource + 8*Q_L*Rload*Xload*Xsource^2 - 4*Q_L*Rload*Xsource^3 + 4*Rsource^2*Xload*Xsource - 4*Xload^2*Xsource^2 + 4*Xload*Xsource^3)^(1/2) - 2*Q_L*Rload*Rsource - 2*Q_C*Xload*Xsource + 2*Q_C*Q_L*Rload*Xsource))/(2*(Q_C^2 + 1)*(Xload - Xsource - Q_L*Rload + Q_L*Rsource))(Published with MATLAB® R2018a)
Note that the output from the Symbolic Math appears as four equations in MATLAB's Command Window:
These equations are paired into XL, XC pairs. The first pair is XL(1), XC(1), and the second pair is XL(2), XC(2). Thus, four different reactances (two inductive, two capacitive) are calculated with these equations. If a CpLs network configuration exists for Zload, then one and only one of these pairs of reactances will have both of its reactance values "real" (no imaginary component) and "positive".
If neither pair have reactances that are both real and positive, then a CpLs configuration does not exist for the given Zload.
Similarly, below is the MATLAB script to calculate XL and XC values for an LsCp low-pass L-network. Note that, again, its inputs are Zload, Zsource, Qinductor and Qcapacitor. The outputs are Xinductor and Xcapacitor.
function [ X_L_Val, X_C_Val ] = ser_L_shunt_C_Q_3(Rload,Xload,Rsource,Xsource,Q_L,Q_C) close clc % Formulas generated using symbolic math contained in the MATLAB script: % SymMath_LsCp_from_Qs_and_Zload_3.m. % First, calculating XL. Note that two values are calculated. X_L_Val(1) = -(Q_L*(Q_C*Rload^2 - 2*Rsource*Xload + Q_L*Rload^2 + (4*Q_C^2*Q_L^2*Rload^3*Rsource - 4*Q_C^2*Q_L^2*Rload^2*Rsource^2 + 4*Q_C^2*Q_L^2*Rload*Rsource*Xload^2 - 4*Q_C^2*Q_L*Rload^3*Xsource + 8*Q_C^2*Q_L*Rload^2*Rsource*Xsource - 4*Q_C^2*Q_L*Rload*Xload^2*Xsource + Q_C^2*Rload^4 + 2*Q_C^2*Rload^2*Xload^2 - 4*Q_C^2*Rload^2*Xsource^2 + Q_C^2*Xload^4 + 4*Q_C*Q_L^2*Rload^2*Rsource*Xload - 8*Q_C*Q_L^2*Rload*Rsource^2*Xload + 4*Q_C*Q_L^2*Rsource*Xload^3 + 2*Q_C*Q_L*Rload^4 - 4*Q_C*Q_L*Rload^3*Rsource + 4*Q_C*Q_L*Rload^2*Xload^2 - 4*Q_C*Q_L*Rload^2*Xload*Xsource - 4*Q_C*Q_L*Rload*Rsource*Xload^2 + 16*Q_C*Q_L*Rload*Rsource*Xload*Xsource + 2*Q_C*Q_L*Xload^4 - 4*Q_C*Q_L*Xload^3*Xsource + 4*Q_C*Rload^3*Xsource + 4*Q_C*Rload*Xload^2*Xsource - 8*Q_C*Rload*Xload*Xsource^2 + Q_L^2*Rload^4 + 2*Q_L^2*Rload^2*Xload^2 - 4*Q_L^2*Rsource^2*Xload^2 + Q_L^2*Xload^4 - 4*Q_L*Rload^2*Rsource*Xload - 4*Q_L*Rsource*Xload^3 + 8*Q_L*Rsource*Xload^2*Xsource + 4*Rload^2*Xload*Xsource + 4*Xload^3*Xsource - 4*Xload^2*Xsource^2)^(1/2) + Q_C*Xload^2 + Q_L*Xload^2 - 2*Q_C*Rload*Rsource - 2*Q_L*Xload*Xsource - 2*Q_C*Q_L*Rload*Xsource))/(2*(Q_L^2 + 1)*(Xload + Q_C*Rload)); X_L_Val(2) = (Q_L*(2*Rsource*Xload - Q_C*Rload^2 - Q_L*Rload^2 + (4*Q_C^2*Q_L^2*Rload^3*Rsource - 4*Q_C^2*Q_L^2*Rload^2*Rsource^2 + 4*Q_C^2*Q_L^2*Rload*Rsource*Xload^2 - 4*Q_C^2*Q_L*Rload^3*Xsource + 8*Q_C^2*Q_L*Rload^2*Rsource*Xsource - 4*Q_C^2*Q_L*Rload*Xload^2*Xsource + Q_C^2*Rload^4 + 2*Q_C^2*Rload^2*Xload^2 - 4*Q_C^2*Rload^2*Xsource^2 + Q_C^2*Xload^4 + 4*Q_C*Q_L^2*Rload^2*Rsource*Xload - 8*Q_C*Q_L^2*Rload*Rsource^2*Xload + 4*Q_C*Q_L^2*Rsource*Xload^3 + 2*Q_C*Q_L*Rload^4 - 4*Q_C*Q_L*Rload^3*Rsource + 4*Q_C*Q_L*Rload^2*Xload^2 - 4*Q_C*Q_L*Rload^2*Xload*Xsource - 4*Q_C*Q_L*Rload*Rsource*Xload^2 + 16*Q_C*Q_L*Rload*Rsource*Xload*Xsource + 2*Q_C*Q_L*Xload^4 - 4*Q_C*Q_L*Xload^3*Xsource + 4*Q_C*Rload^3*Xsource + 4*Q_C*Rload*Xload^2*Xsource - 8*Q_C*Rload*Xload*Xsource^2 + Q_L^2*Rload^4 + 2*Q_L^2*Rload^2*Xload^2 - 4*Q_L^2*Rsource^2*Xload^2 + Q_L^2*Xload^4 - 4*Q_L*Rload^2*Rsource*Xload - 4*Q_L*Rsource*Xload^3 + 8*Q_L*Rsource*Xload^2*Xsource + 4*Rload^2*Xload*Xsource + 4*Xload^3*Xsource - 4*Xload^2*Xsource^2)^(1/2) - Q_C*Xload^2 - Q_L*Xload^2 + 2*Q_C*Rload*Rsource + 2*Q_L*Xload*Xsource + 2*Q_C*Q_L*Rload*Xsource))/(2*(Q_L^2 + 1)*(Xload + Q_C*Rload)); % Then, calculating XC. Note that two values are calculated. X_C_Val(1) = (Q_C*(2*Rload*Xsource + Q_C*Rload^2 + Q_L*Rload^2 + (4*Q_C^2*Q_L^2*Rload^3*Rsource - 4*Q_C^2*Q_L^2*Rload^2*Rsource^2 + 4*Q_C^2*Q_L^2*Rload*Rsource*Xload^2 - 4*Q_C^2*Q_L*Rload^3*Xsource + 8*Q_C^2*Q_L*Rload^2*Rsource*Xsource - 4*Q_C^2*Q_L*Rload*Xload^2*Xsource + Q_C^2*Rload^4 + 2*Q_C^2*Rload^2*Xload^2 - 4*Q_C^2*Rload^2*Xsource^2 + Q_C^2*Xload^4 + 4*Q_C*Q_L^2*Rload^2*Rsource*Xload - 8*Q_C*Q_L^2*Rload*Rsource^2*Xload + 4*Q_C*Q_L^2*Rsource*Xload^3 + 2*Q_C*Q_L*Rload^4 - 4*Q_C*Q_L*Rload^3*Rsource + 4*Q_C*Q_L*Rload^2*Xload^2 - 4*Q_C*Q_L*Rload^2*Xload*Xsource - 4*Q_C*Q_L*Rload*Rsource*Xload^2 + 16*Q_C*Q_L*Rload*Rsource*Xload*Xsource + 2*Q_C*Q_L*Xload^4 - 4*Q_C*Q_L*Xload^3*Xsource + 4*Q_C*Rload^3*Xsource + 4*Q_C*Rload*Xload^2*Xsource - 8*Q_C*Rload*Xload*Xsource^2 + Q_L^2*Rload^4 + 2*Q_L^2*Rload^2*Xload^2 - 4*Q_L^2*Rsource^2*Xload^2 + Q_L^2*Xload^4 - 4*Q_L*Rload^2*Rsource*Xload - 4*Q_L*Rsource*Xload^3 + 8*Q_L*Rsource*Xload^2*Xsource + 4*Rload^2*Xload*Xsource + 4*Xload^3*Xsource - 4*Xload^2*Xsource^2)^(1/2) + Q_C*Xload^2 + Q_L*Xload^2 - 2*Q_L*Rload*Rsource - 2*Q_C*Xload*Xsource + 2*Q_C*Q_L*Rsource*Xload))/(2*(Q_C^2 + 1)*(Xload - Xsource - Q_L*Rload + Q_L*Rsource)); X_C_Val(2) = (Q_C*(2*Rload*Xsource + Q_C*Rload^2 + Q_L*Rload^2 - (4*Q_C^2*Q_L^2*Rload^3*Rsource - 4*Q_C^2*Q_L^2*Rload^2*Rsource^2 + 4*Q_C^2*Q_L^2*Rload*Rsource*Xload^2 - 4*Q_C^2*Q_L*Rload^3*Xsource + 8*Q_C^2*Q_L*Rload^2*Rsource*Xsource - 4*Q_C^2*Q_L*Rload*Xload^2*Xsource + Q_C^2*Rload^4 + 2*Q_C^2*Rload^2*Xload^2 - 4*Q_C^2*Rload^2*Xsource^2 + Q_C^2*Xload^4 + 4*Q_C*Q_L^2*Rload^2*Rsource*Xload - 8*Q_C*Q_L^2*Rload*Rsource^2*Xload + 4*Q_C*Q_L^2*Rsource*Xload^3 + 2*Q_C*Q_L*Rload^4 - 4*Q_C*Q_L*Rload^3*Rsource + 4*Q_C*Q_L*Rload^2*Xload^2 - 4*Q_C*Q_L*Rload^2*Xload*Xsource - 4*Q_C*Q_L*Rload*Rsource*Xload^2 + 16*Q_C*Q_L*Rload*Rsource*Xload*Xsource + 2*Q_C*Q_L*Xload^4 - 4*Q_C*Q_L*Xload^3*Xsource + 4*Q_C*Rload^3*Xsource + 4*Q_C*Rload*Xload^2*Xsource - 8*Q_C*Rload*Xload*Xsource^2 + Q_L^2*Rload^4 + 2*Q_L^2*Rload^2*Xload^2 - 4*Q_L^2*Rsource^2*Xload^2 + Q_L^2*Xload^4 - 4*Q_L*Rload^2*Rsource*Xload - 4*Q_L*Rsource*Xload^3 + 8*Q_L*Rsource*Xload^2*Xsource + 4*Rload^2*Xload*Xsource + 4*Xload^3*Xsource - 4*Xload^2*Xsource^2)^(1/2) + Q_C*Xload^2 + Q_L*Xload^2 - 2*Q_L*Rload*Rsource - 2*Q_C*Xload*Xsource + 2*Q_C*Q_L*Rsource*Xload))/(2*(Q_C^2 + 1)*(Xload - Xsource - Q_L*Rload + Q_L*Rsource)); end
(Published with MATLAB® R2018a)
And below is the MATLAB script (written in large part by Dick Benson, W1QG), using the Symbolic Math Toolbox, that created the four equations, above:
% Script Name: SymMath_LsCp_from_Qs_and_Zload_3.m % SYMBOLIC Analysis .... work from Source to Load to get Zin % Source, Series L then Shunt C , then load % This version uses X_C instead of B_C (modified by k6jca) % Make sure the 'syms' line, below is terminated with "real"! syms Rsource Xsource Rload Xload X_L Q_L X_C Q_C real Zshunt = 1/(1/(X_C/Q_C - (1i*X_C)) + 1/((Rload + 1i*Xload))); % Rs = Xs/Q Zin = X_L/Q_L + 1i*X_L + Zshunt; eq1 = simplify(real(Zin),'Criterion','preferReal','Steps',50); eq2 = simplify(imag(Zin),'Criterion','preferReal','Steps',50); [X_L_Sol, X_C_Sol] = solve([eq1==Rsource,eq2==Xsource],[X_L,X_C]); XLS = simplify(X_L_Sol,'Steps',50) XCS = simplify(X_C_Sol,'Steps',50) % The resulting four equations will appear in MATLAB's % Command Window, from which they are copied and then % pasted into the script: ser_L_shunt_C_Q_3.m
XLS = -(Q_L*(Q_C*Rload^2 - 2*Rsource*Xload + Q_L*Rload^2 + (4*Q_C^2*Q_L^2*Rload^3*Rsource - 4*Q_C^2*Q_L^2*Rload^2*Rsource^2 + 4*Q_C^2*Q_L^2*Rload*Rsource*Xload^2 - 4*Q_C^2*Q_L*Rload^3*Xsource + 8*Q_C^2*Q_L*Rload^2*Rsource*Xsource - 4*Q_C^2*Q_L*Rload*Xload^2*Xsource + Q_C^2*Rload^4 + 2*Q_C^2*Rload^2*Xload^2 - 4*Q_C^2*Rload^2*Xsource^2 + Q_C^2*Xload^4 + 4*Q_C*Q_L^2*Rload^2*Rsource*Xload - 8*Q_C*Q_L^2*Rload*Rsource^2*Xload + 4*Q_C*Q_L^2*Rsource*Xload^3 + 2*Q_C*Q_L*Rload^4 - 4*Q_C*Q_L*Rload^3*Rsource + 4*Q_C*Q_L*Rload^2*Xload^2 - 4*Q_C*Q_L*Rload^2*Xload*Xsource - 4*Q_C*Q_L*Rload*Rsource*Xload^2 + 16*Q_C*Q_L*Rload*Rsource*Xload*Xsource + 2*Q_C*Q_L*Xload^4 - 4*Q_C*Q_L*Xload^3*Xsource + 4*Q_C*Rload^3*Xsource + 4*Q_C*Rload*Xload^2*Xsource - 8*Q_C*Rload*Xload*Xsource^2 + Q_L^2*Rload^4 + 2*Q_L^2*Rload^2*Xload^2 - 4*Q_L^2*Rsource^2*Xload^2 + Q_L^2*Xload^4 - 4*Q_L*Rload^2*Rsource*Xload - 4*Q_L*Rsource*Xload^3 + 8*Q_L*Rsource*Xload^2*Xsource + 4*Rload^2*Xload*Xsource + 4*Xload^3*Xsource - 4*Xload^2*Xsource^2)^(1/2) + Q_C*Xload^2 + Q_L*Xload^2 - 2*Q_C*Rload*Rsource - 2*Q_L*Xload*Xsource - 2*Q_C*Q_L*Rload*Xsource))/(2*(Q_L^2 + 1)*(Xload + Q_C*Rload)) (Q_L*(2*Rsource*Xload - Q_C*Rload^2 - Q_L*Rload^2 + (4*Q_C^2*Q_L^2*Rload^3*Rsource - 4*Q_C^2*Q_L^2*Rload^2*Rsource^2 + 4*Q_C^2*Q_L^2*Rload*Rsource*Xload^2 - 4*Q_C^2*Q_L*Rload^3*Xsource + 8*Q_C^2*Q_L*Rload^2*Rsource*Xsource - 4*Q_C^2*Q_L*Rload*Xload^2*Xsource + Q_C^2*Rload^4 + 2*Q_C^2*Rload^2*Xload^2 - 4*Q_C^2*Rload^2*Xsource^2 + Q_C^2*Xload^4 + 4*Q_C*Q_L^2*Rload^2*Rsource*Xload - 8*Q_C*Q_L^2*Rload*Rsource^2*Xload + 4*Q_C*Q_L^2*Rsource*Xload^3 + 2*Q_C*Q_L*Rload^4 - 4*Q_C*Q_L*Rload^3*Rsource + 4*Q_C*Q_L*Rload^2*Xload^2 - 4*Q_C*Q_L*Rload^2*Xload*Xsource - 4*Q_C*Q_L*Rload*Rsource*Xload^2 + 16*Q_C*Q_L*Rload*Rsource*Xload*Xsource + 2*Q_C*Q_L*Xload^4 - 4*Q_C*Q_L*Xload^3*Xsource + 4*Q_C*Rload^3*Xsource + 4*Q_C*Rload*Xload^2*Xsource - 8*Q_C*Rload*Xload*Xsource^2 + Q_L^2*Rload^4 + 2*Q_L^2*Rload^2*Xload^2 - 4*Q_L^2*Rsource^2*Xload^2 + Q_L^2*Xload^4 - 4*Q_L*Rload^2*Rsource*Xload - 4*Q_L*Rsource*Xload^3 + 8*Q_L*Rsource*Xload^2*Xsource + 4*Rload^2*Xload*Xsource + 4*Xload^3*Xsource - 4*Xload^2*Xsource^2)^(1/2) - Q_C*Xload^2 - Q_L*Xload^2 + 2*Q_C*Rload*Rsource + 2*Q_L*Xload*Xsource + 2*Q_C*Q_L*Rload*Xsource))/(2*(Q_L^2 + 1)*(Xload + Q_C*Rload)) XCS = (Q_C*(2*Rload*Xsource + Q_C*Rload^2 + Q_L*Rload^2 + (4*Q_C^2*Q_L^2*Rload^3*Rsource - 4*Q_C^2*Q_L^2*Rload^2*Rsource^2 + 4*Q_C^2*Q_L^2*Rload*Rsource*Xload^2 - 4*Q_C^2*Q_L*Rload^3*Xsource + 8*Q_C^2*Q_L*Rload^2*Rsource*Xsource - 4*Q_C^2*Q_L*Rload*Xload^2*Xsource + Q_C^2*Rload^4 + 2*Q_C^2*Rload^2*Xload^2 - 4*Q_C^2*Rload^2*Xsource^2 + Q_C^2*Xload^4 + 4*Q_C*Q_L^2*Rload^2*Rsource*Xload - 8*Q_C*Q_L^2*Rload*Rsource^2*Xload + 4*Q_C*Q_L^2*Rsource*Xload^3 + 2*Q_C*Q_L*Rload^4 - 4*Q_C*Q_L*Rload^3*Rsource + 4*Q_C*Q_L*Rload^2*Xload^2 - 4*Q_C*Q_L*Rload^2*Xload*Xsource - 4*Q_C*Q_L*Rload*Rsource*Xload^2 + 16*Q_C*Q_L*Rload*Rsource*Xload*Xsource + 2*Q_C*Q_L*Xload^4 - 4*Q_C*Q_L*Xload^3*Xsource + 4*Q_C*Rload^3*Xsource + 4*Q_C*Rload*Xload^2*Xsource - 8*Q_C*Rload*Xload*Xsource^2 + Q_L^2*Rload^4 + 2*Q_L^2*Rload^2*Xload^2 - 4*Q_L^2*Rsource^2*Xload^2 + Q_L^2*Xload^4 - 4*Q_L*Rload^2*Rsource*Xload - 4*Q_L*Rsource*Xload^3 + 8*Q_L*Rsource*Xload^2*Xsource + 4*Rload^2*Xload*Xsource + 4*Xload^3*Xsource - 4*Xload^2*Xsource^2)^(1/2) + Q_C*Xload^2 + Q_L*Xload^2 - 2*Q_L*Rload*Rsource - 2*Q_C*Xload*Xsource + 2*Q_C*Q_L*Rsource*Xload))/(2*(Q_C^2 + 1)*(Xload - Xsource - Q_L*Rload + Q_L*Rsource)) (Q_C*(2*Rload*Xsource + Q_C*Rload^2 + Q_L*Rload^2 - (4*Q_C^2*Q_L^2*Rload^3*Rsource - 4*Q_C^2*Q_L^2*Rload^2*Rsource^2 + 4*Q_C^2*Q_L^2*Rload*Rsource*Xload^2 - 4*Q_C^2*Q_L*Rload^3*Xsource + 8*Q_C^2*Q_L*Rload^2*Rsource*Xsource - 4*Q_C^2*Q_L*Rload*Xload^2*Xsource + Q_C^2*Rload^4 + 2*Q_C^2*Rload^2*Xload^2 - 4*Q_C^2*Rload^2*Xsource^2 + Q_C^2*Xload^4 + 4*Q_C*Q_L^2*Rload^2*Rsource*Xload - 8*Q_C*Q_L^2*Rload*Rsource^2*Xload + 4*Q_C*Q_L^2*Rsource*Xload^3 + 2*Q_C*Q_L*Rload^4 - 4*Q_C*Q_L*Rload^3*Rsource + 4*Q_C*Q_L*Rload^2*Xload^2 - 4*Q_C*Q_L*Rload^2*Xload*Xsource - 4*Q_C*Q_L*Rload*Rsource*Xload^2 + 16*Q_C*Q_L*Rload*Rsource*Xload*Xsource + 2*Q_C*Q_L*Xload^4 - 4*Q_C*Q_L*Xload^3*Xsource + 4*Q_C*Rload^3*Xsource + 4*Q_C*Rload*Xload^2*Xsource - 8*Q_C*Rload*Xload*Xsource^2 + Q_L^2*Rload^4 + 2*Q_L^2*Rload^2*Xload^2 - 4*Q_L^2*Rsource^2*Xload^2 + Q_L^2*Xload^4 - 4*Q_L*Rload^2*Rsource*Xload - 4*Q_L*Rsource*Xload^3 + 8*Q_L*Rsource*Xload^2*Xsource + 4*Rload^2*Xload*Xsource + 4*Xload^3*Xsource - 4*Xload^2*Xsource^2)^(1/2) + Q_C*Xload^2 + Q_L*Xload^2 - 2*Q_L*Rload*Rsource - 2*Q_C*Xload*Xsource + 2*Q_C*Q_L*Rsource*Xload))/(2*(Q_C^2 + 1)*(Xload - Xsource - Q_L*Rload + Q_L*Rsource))
(Published with MATLAB® R2018a)
L-Network Designer:
With these functions I created my own L-Network Designer script in MATLAB:
% k6jca % L-Network Designer: Determines L and C and % Lowpass L-network Configuration (LsCp or CpLs) % Given Zsource, Zload, QL, QC, and Frequency. clear all close all clc Zo = 50; % Inputs (F, Rsource, Xsource, Q_L, Q_C, Rload,Xload) F = 3.5e6; % Frequency (Hz) Rs = Zo; % Rsource (most likely this will be 50 ohms) Xs = 0; % Xsource (most likely this will be 0) QL = 100; % inductor Q QC = 100; % capacitor Q Rld = 16.47; % Rload Xld = 74.46; % Xload % Rld = 7.079; % Rload % Xld = -32.01; % Xload w = 2*pi*F; Zs = Rs + 1i*Xs; % source impedance Zload = Rld + 1i*Xld; % load impedance % Given Zload, Zsource (which is 50 ohms here), Ql and Qc, % calculate the XL and XC values of the LsCp or CpLs % network than will match Zload to Zsource. % % Note that for an LsCp network, two XL and two XC terms % are returned for each load. Ditto for the CpLs network. % (Note that the equations in the called functions were % derived by MATLAB using symbolic math). [LsCp_XL, LsCp_XC] = ser_L_shunt_C_Q_3(Rld,Xld,Rs,Xs,QL,QC); [CpLs_XL, CpLs_XC] = shunt_C_ser_L_Q_3(Rld,Xld,Rs,Xs,QL,QC); % of the four pairs of XL and XC terms returnd by the % functions(each function call returns two pairs), but % only one pair is valid. This pair will have % no imaginary components (that is, neither XL or XC is a % complex number)and both XL and XC will be positive. % % So let's first check each XL and each XC and identify % which of these are real (not complex) and positive. if(isreal(LsCp_XL(1)) && real(LsCp_XL(1)) > 0) itsValid(1) = 1; else itsValid(1) = 0; end if(isreal(LsCp_XL(2)) && real(LsCp_XL(2)) > 0) itsValid(2) = 1; else itsValid(2) = 0; end if(isreal(LsCp_XC(1)) && real(LsCp_XC(1)) > 0) itsValid(3) = 1; else itsValid(3) = 0; end if(isreal(LsCp_XC(2)) && real(LsCp_XC(2)) > 0) itsValid(4) = 1; else itsValid(4) = 0; end if(isreal(CpLs_XL(1)) && real(CpLs_XL(1)) > 0) itsValid(5) = 1; else itsValid(5) = 0; end if(isreal(CpLs_XL(2)) && real(CpLs_XL(2)) > 0) itsValid(6) = 1; else itsValid(6) = 0; end if(isreal(CpLs_XC(1)) && real(CpLs_XC(1)) > 0) itsValid(7) = 1; else itsValid(7) = 0; end if(isreal(CpLs_XC(2)) && real(CpLs_XC(2)) > 0) itsValid(8) = 1; else itsValid(8) = 0; end % Next, we are looking for "pairs" of XL and XC that % are valid. Only one pair should be valid. The other % three pairs should be invalid. % For example, the first check below will be to check % XL(1) and XC(1) for LsCp networks and see if % these values are both valid. if(itsValid(1) && itsValid(3)) Lnet_id = 'LsCp' XL = LsCp_XL(1); XC = LsCp_XC(1); elseif(itsValid(2) && itsValid(4)) % XL(2),XC(2),LsCp netwrk Lnet_id = 'LsCp' XL = LsCp_XL(2); XC = LsCp_XC(2); elseif(itsValid(5) && itsValid(7)) % XL(1),XC(1),CpLs netwrk Lnet_id = 'CpLs' XL = CpLs_XL(1); XC = CpLs_XC(1); elseif(itsValid(6) && itsValid(8)) % XL(2),XC(2),CpLs netwrk Lnet_id = 'CpLs' XL = CpLs_XL(2); XC = CpLs_XC(2); else % if there are no valid pairs (which OUGHT NOT OCCUR... Lnet_id = 'None!' % just flag there's a problem. disp('huh?'); end % from XL and XC, calculate Ls and Cp Ls = XL/w Cp = 1/(XC*w) % and calculate the S-parameters based upon whether the % valid pair is for an LsCp network or for a CpLs network... if(Lnet_id == 'LsCp') Spar = S_LsCp(Ls,QL,Cp,QC, Zo, F); else Spar = S_CpLs(Ls,QL,Cp,QC, Zo, F); end % With these, calculate network power loss Gp_Lnet = powergain(Spar,Zo,Zload,'Gp') Gp_dBLoss = 10*log10(Gp_Lnet); Gp_Percent_Loss = (1-Gp_Lnet)*100
Lnet_id =
'LsCp'
Ls =
5.3255e-06
Cp =
9.1308e-10
Gp_Lnet =
0.9119
Gp_Percent_Loss =
8.8073
(Published with MATLAB® R2018a)
Note that my MATLAB script uses the following two functions, written by Dick Benson, W1QG, that create S-parameters for the LsCp and CpLs L-networks:
function S_LsCp():
function S = S_LsCp(L, Ql, C, Qc, Zo, f ) % Written by W1QG % From Symbolc Math in S_Parameters_for_L_Networks.m results. % S Parameters for LsCp configuration. w=2*pi*f; dxx=(Ql*Zo*2i + L*w*1i + 2*Qc*Ql*Zo + L*Qc*w - L*Ql*w + L*Qc*Ql*w*1i + C*L*Qc*Zo*w^2*1i + C*Qc*Ql*Zo^2*w*1i - C*L*Qc*Ql*Zo*w^2); S11_LsCp = (w*(L*1i + L*Qc - L*Ql + L*Qc*Ql*1i - C*Qc*Ql*Zo^2*1i + C*L*Qc*Zo*w*1i - C*L*Qc*Ql*Zo*w))/ dxx; S12_LsCp = -(Ql*Zo*(Qc + 1i)*2i)/ (2*Ql*Zo + L*w - Qc*Ql*Zo*2i - L*Qc*w*1i + L*Ql*w*1i + L*Qc*Ql*w + C*L*Qc*Zo*w^2 + C*Qc*Ql*Zo^2*w + C*L*Qc*Ql*Zo*w^2*1i); % S21_LsCp = -(2*Ql*Zo*(- 1 + Qc*1i))/(2*Ql*Zo + L*w - Qc*Ql*Zo*2i - L*Qc*w*1i + L*Ql*w*1i + L*Qc*Ql*w + C*L*Qc*Zo*w^2 + C*Qc*Ql*Zo^2*w + C*L*Qc*Ql*Zo*w^2*1i); S21_LsCp = S12_LsCp; S22_LsCp = (w*(L*1i + L*Qc - L*Ql + L*Qc*Ql*1i - C*Qc*Ql*Zo^2*1i - C*L*Qc*Zo*w*1i + C*L*Qc*Ql*Zo*w))/dxx; S = [S11_LsCp,S12_LsCp; S21_LsCp,S22_LsCp]; endfunction S_CpLs():
(Published with MATLAB® R2018a)
function S = S_CpLs(L, Ql, C, Qc, Zo, f ) % Written by W1QG % From Symbolc Math in S_Parameters_for_L_Networks.m results. % S Parameters for CpLs configuration. w=2*pi*f; dxx = (Ql*Zo*2i + L*w*1i + 2*Qc*Ql*Zo + L*Qc*w - L*Ql*w + L*Qc*Ql*w*1i + C*L*Qc*Zo*w^2*1i + C*Qc*Ql*Zo^2*w*1i - C*L*Qc*Ql*Zo*w^2); S11_CpLs = (w*(L*1i + L*Qc - L*Ql + L*Qc*Ql*1i - C*Qc*Ql*Zo^2*1i - C*L*Qc*Zo*w*1i + C*L*Qc*Ql*Zo*w))/dxx; S22_CpLs = (w*(L*1i + L*Qc - L*Ql + L*Qc*Ql*1i - C*Qc*Ql*Zo^2*1i + C*L*Qc*Zo*w*1i - C*L*Qc*Ql*Zo*w))/dxx; S12_CpLs = -(2*Ql*Zo*(- 1 + Qc*1i))/(2*Ql*Zo + L*w - Qc*Ql*Zo*2i - L*Qc*w*1i + L*Ql*w*1i + L*Qc*Ql*w + C*L*Qc*Zo*w^2 + C*Qc*Ql*Zo^2*w + C*L*Qc*Ql*Zo*w^2*1i); % S21_CpLs = -(2*Ql*Zo*(- 1 + Qc*1i))/(2*Ql*Zo + L*w - Qc*Ql*Zo*2i - L*Qc*w*1i + L*Ql*w*1i + L*Qc*Ql*w + C*L*Qc*Zo*w^2 + C*Qc*Ql*Zo^2*w + C*L*Qc*Ql*Zo*w^2*1i) S21_CpLs=S12_CpLs; S = [S11_CpLs, S12_CpLs; S21_CpLs,S22_CpLs]; end
(Published with MATLAB® R2018a)
Conclusion:
This post presents low-pass L-network design equations that include component loss.
These equations were derived using MATLAB's Symbolic Math Toolbox, which provides a powerful tool for generating equations that might be too complex for mere pencil-and-paper derivation using standard Circuit Analysis techniques.
A similar technique can be used to derive lossy L-network design equations for other L-network configurations (e.g. high-pass LpCs, CsLp, etc.). I would encourage the interested reader to do so!
Antenna Tuner Blog Posts:
A quick tutorial on Smith Chart basics:
http://k6jca.blogspot.com/2015/03/a-brief-tutorial-on-smith-charts.html
Plotting Smith Chart Data in 3-D:
http://k6jca.blogspot.com/2018/09/plotting-3-d-smith-charts-with-matlab.html
The L-network:
http://k6jca.blogspot.com/2015/03/notes-on-antenna-tuners-l-network-and.html
A correction to the usual L-network design constraints:
http://k6jca.blogspot.com/2015/04/revisiting-l-network-equations-and.html
Calculating L-Network values when the components are lossy :
http://k6jca.blogspot.com/2018/09/l-networks-new-equations-for-better.html
A look at highpass T-Networks:
http://k6jca.blogspot.com/2015/04/notes-on-antenna-tuners-t-network-part-1.html
More on the W8ZR EZ-Tuner:
http://k6jca.blogspot.com/2015/05/notes-on-antenna-tuners-more-on-w8zr-ez.html (Note that this tuner is also discussed in the highpass T-Network post).
The Elecraft KAT-500:
http://k6jca.blogspot.com/2015/05/notes-on-antenna-tuners-elecraft-kat500.html
The Nye Viking MB-V-A tuner and the Rohde Coupler:
http://k6jca.blogspot.com/2015/05/notes-on-antenna-tuners-nye-viking-mb-v.html
http://k6jca.blogspot.com/2018/08/notes-on-antenna-tuners-drake-mn-4.html
Measuring a Tuner's "Match-Space":
Measuring Tuner Power Loss:
As always, I might have made a mistake in my equations, assumptions, drawings, or interpretations. If you see anything you believe to be in error or if anything is confusing, please feel free to contact me or comment below.
And so I should add -- this information is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE.



























2 comments:
You might point out that SimSmith's L matching element does exactly this which is to say: it transforms one arbitrary, complex input impedance into another arbitrary, complex impedance and takes Q into account.
Thanks very much, Ward. Your comment is now attached to the blog!
Best regards,
Jeff
Post a Comment