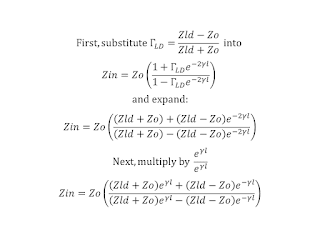This third technique (the other two are here and here) for finding a transmission line's Zo is based upon the concept of "Circles of Constant SWR"
I've used this technique in the past to find the Zo of twisted-pair I had made from 14 AWG Stranded THHN wire (see this 2018 blogpost), per the image, below:
The Concept of Circles of Constant-SWR:
If a transmission line is terminated in a load not equal to the line's Characteristic Impedance Zo, there will be a voltage (and a current) Standing-Wave on the transmission line, and the impedance seen at the input end of the transmission line will be a function of the frequency, the line's length, its characteristics (e.g. Zo, loss, and phase delay), and the load impedance.
As frequency changes, so does the impedance seen at the input end of the transmission line, because the signal's round-trip phase shift on the transmission line changes (i.e. as frequency changes so does the apparent length of the line, if length is defined in terms of wavelengths).
If we were plot on a Smith Chart, as frequency changes, the Reflection Coefficient (Γ) representing Zin of the transmission line, we would see a locus of points representing different Zin impedances.
If the transmission line is lossless, then as the frequency changes, the Reflection Coefficients representing these impedances form a circle -- a Circle of Constant SWR, centered on Zo of the transmission line.
You might be familiar with circles of constant SWR circling around a Smith Chart's center-point (typically the 50 + j0 ohm point).
An example of a circle of constant SWR centered on a 50-ohm Smith Chart is shown below, simulated with SimSmith. Note that the coax is an ideal (lossless) 50 ohms and the load is 25 ohms.
At 0 Hz, (i.e. 9 o'clock on the chart) the measured S11 value represents a Zin impedance of 25 + j0 ohms. And halfway around the circle, at the 3 o'clock position, the measured S11 value represents a Zin impedance of 100 ohms. Note that all of the impedances on the circle have the same SWR, referenced to a Zo of 50 ohms, and these are all impedances we would see at the input of the lossless transmission line as the frequency is changed.
To calculate Zo from the circle, it is simplest to chose the two points opposite each other on the "real-only" axis of the Smith Chart, where the reactance of each Zin is 0. Zo is then just the geometric mean of the two Zin resistance values (because Zin has no reactance if on the "real-only" axis).
In the example above, the two resistance values are 25 and 100 ohms. The Zo calculation is:
Zo = SQRT(25*100) = 50 ohms
This concept SWR circles can be extended to transmission lines of other impedances, too, even when plotted on a Smith Chart referenced to 50 ohms, but the circles will now be centered around Zo of the coax being measured, rather than the Smith Chart's reference Zo.
Circles of Constant SWR when Zo of a Lossless Line is NOT 50 ohms:
The concept of Circles of Constant SWR still applies even if Zo of the Transmission Line is not 50 ohms. If the line is lossless, SWR depends solely upon the line's Zo and the Load impedance.
If we were to measure the impedance looking into the input (Zin) side of the Transmission Line (using a VNA, for example), as frequency changes we would see Zin (calculated from measured S11) trace a circle. But the circle now would be centered on the Zo of our transmission line.
And this is the third technique we can use to find Zo of a unknown transmission line. Terminate the line with a known impedance (not equal to Zo -- we need some SWR, otherwise there is no circle!) and next plot S11 over frequency on the Smith Chart.
If the line is lossless, the resulting plot will be a circle centered on the new Zo, and Zo can be found by taking the square-root of the impedances calculated from the S11 measurements at these two points opposite each other (180 degrees apart) on the circle. If the circle's center lies on the Smith Chart's "real only" axis, then it is easiest just to use the resistances at the 3 and 9 o'clock positions on the circle, where the reactance of either Zin value is 0.
The example, shown below, shows circles of constant SWR for a transmission line whose Zo is 75 ohms and which, in one case, is terminated with 50 ohms, and in the other case terminated with 300 ohms. You can see that the geometric means of impedances opposite each other on either unit circle calculate to be 75 ohms, the Zo of the transmission line, independent of which SWR circle is used.
Circles of Constant SWR for Lossy Lines:
If the line is lossy the plotted S11 values will no longer trace a perfect circle on the Smith Chart as frequency is varied. Instead, they will form a spiral which spirals, as frequency increases, inwards towards the Zo of the lossy transmission line.
Thus, we no longer have perfect circles of constant SWR (we have a spiral, instead), and choosing two points opposite on the spiral (e.g. both on the real-only axis) will give us a calculated value close to the transmission line's actual Zo, but it will not be perfect.
The less the line loss, however, the more accurate the calculation will be.
Below is a plot showing a simulated example of Belden 8241 75 ohm coax terminated with 50 ohms. Included is also the constant SWR circle (in yellow) for the same load, but assuming ideal, lossless, coax.
If the load is changed from 50 ohms to 300 ohms, the lossy coax's spiral is larger and thus more obvious.
Resources:
More on the underlying "lossless line" math can be found, here: Munk, Ben A., Metamaterials: Critique and Alternatives, Wiley Online Library, Appendix C, How to Measure the Characteristic Impedance and Attenuation of a Cable
Standard Caveat:
As always, I might have made a mistake in my equations, assumptions, drawings,
or interpretations. If you see anything you believe to be in error or if
anything is confusing, please feel free to contact me or comment below.
And
so I should add -- this information is distributed in the hope that it will be
useful, but WITHOUT ANY WARRANTY; without even the implied warranty of
MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE.
here






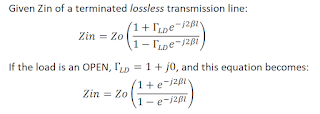

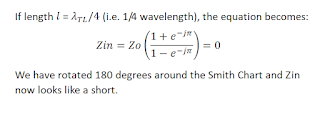




































%20test%20with%20actual%20SO.png)