A common equation for calculating Zin of a terminated transmission line uses complex exponentials. But now and again I come across an equivalent equation that instead uses the hyperbolic tangent function, tanh().
I have never used hyperbolic trig functions as an engineer -- in fact, the only time I've come across them is with respect to transmission lines, and personally, I find the complex-exponential form of these equations much more intuitive, given how common complex exponentials are used in electrical engineering.
This blog post shows how the tanh() form of the equation for Zin, the input impedance of a terminated lossy transmission line, can be derived from the complex-exponential equation.
Also, I will show how, for a lossless transmission line, the tanh() equation reduces to one using tangent (tan()) functions.
I'll start out this post with the lossy-line's complex-exponential equation for Zin, which is:
Zin = Zo*(1 + Γ*e^(-2*γ*l)) / (1 - Γ*e^(-2*γ*l)),
where Γ = (Zload - Zo) / (Zload + Zo), γ = α + jβ, and l = length. Note that α represents loss and jβ represents phase-shift as a signal travels along a transmission line.
And later in this post I'll do the same for the lossless line, whose complex-exponential equation is:
Zin = Zo*(1 + Γ*e^(-j2*β*l)) / (1 - Γ*e^(-j2*β*l)),
That's it!
Standard Caveat:
As always, I might have made a mistake in my equations, assumptions, drawings,
or interpretations. If you see anything you believe to be in error or if
anything is confusing, please feel free to contact me or comment below.
And
so I should add -- this information is distributed in the hope that it will be
useful, but WITHOUT ANY WARRANTY; without even the implied warranty of
MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE.





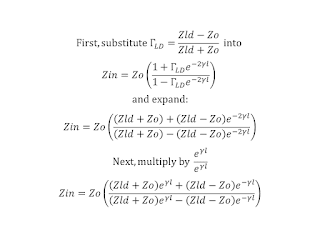




















No comments:
Post a Comment