SPICE is a handy tool for evaluating circuits without having to first
breadboard them, and through its "directives," it provides a powerful method
for analyzing how a circuit might perform with components exhibiting
real-world tolerances.
One such method of "real-world" analysis is Monte Carlo analysis, which, with each new analysis run, randomly varies parameters (within their user-defined limits) to give the user a useful picture of actual circuit performance.
However, as a circuit designer, I'm most often interested in worst-case performance. That is, I want to know how a circuit performs at the extremes of component values, to ensure that I've met whatever design specification I'm designing to. And although Monte Carlo analysis can tell me what the performance is at these limits, if the circuit contains many components, it can take quite a lot of runs before its random selection of parameter values happens to simultaneously correspond to the worst-case limits of all of the components (and it's quite possible that I'll never see the true worst-case limits -- after all, it's a matter of chance).
To truly evaluate performance at a circuit's worst-case limits, we can perform a "worst-case" analysis in lieu of a Monte Carlo analysis. This analysis has an added advantage, too, in that not as many runs are required to ensure that we've truly evaluated all of the components over all possible variations in their tolerances -- after all, we don't need to measure between the tolerances limits (which is what Monte Carlo analysis does). For example, if one of the components is a 10K ohm resistor with a 5% tolerance, worst-case analysis will only use resistance values of 10.5K and 9.5K for this component and not any other value between these limits (whereas Monte Carlo analysis would randomly use any value between, and including, these limits).
Linear Technology's LTSpice can handle both Monte Carlo analysis as well as worst-case analysis. Unfortunately, it's not obvious how to do this from their "Help Topics." For example, "Monte Carlo", when entered into LTSpice's search field, returns no results. Not much use, that!
Nevertheless, LTSpice does indeed have a pre-defined Monte Carlo function. This is the "mc" function, and a search of the Help Topics for "mc" will point to the .PARAM topic, and under this heading we find the function mc (x,y), which, when invoked, returns a "random number between x*(1+y) and x*(1-y) with uniform distribution."
To use this function, rather than define a resistor's value as, say, 10K, we define it as "{mc(10K,0.05)}", where 10K is its nominal value, and 0.05 is its tolerance (5%). (An example will follow below).
OK, so the predefined mc function handles Monte Carlo analysis, but there is no pre-defined "worst case" function. We need to create this ourselves, but it's not too difficult. This can be done using Spice's ".function" directive. Here's an example of a function for worst-case analysis (we'll use this later, too):
.function wc(nom,tola) if (run == 1, nom, if(flat(1)>0,nom*(1+tola),nom*(1-tola)))
In this definition:
- .function is the Spice directive for defining a function.
- wc is the name I've given this instance of this worst-case function.
- nom is the "nominal" value (e.g. 10K for a 10K resistor).
- tola is the tolerance (defined elsewhere with a .param directive (e.g. 0.1 for a 10% tolerance)).
- run is a variable (defined elsewhere in the .step directive) identifying the current run count).
- flat(1) is a Spice function that returns a random number between -1 and 1.
Take as an example a 10K ohm resistor. Normally, we'd just label its value in the LTSpice schematic as "10K". However, to vary its value between its worst-case values, we instead use a more complex label for its value. Rather than entering "10K", in this case we'll enter "{wc_a(10K,tola)}" into the component's value field. (Note the use of the curlicue brackets).
So what happens when we run the analysis?
If this is the first analysis run (run is defined elsewhere in the .step directive and simply is the current run being performed), then, because run = 1, the function returns the value assigned to nom, in this case, 10K.
But for each new run after the first run, and for each component defined with a wc_a function, the function flat(1) is re-evaluated for that component. If the random result returned from flat(1) is greater than 0, then the tolerance is added to the component's nominal value (e.g. for a resistor whose nominal (nom) value is 10K, if tola is 0.1 (10% tolerance), the resistor's value is set to 11K). Otherwise, the tolerance is subtracted from the component's nominal value (e.g. the 10K resistor is set to 9K).
Here's a demonstration of both Monte Carlo and Worst Case analysis. Consider this basic circuit:
(Click on image to enlarge)
Given these component values, a frequency sweep of the input from 1 Hz to 1KHz shows that the circuit has the following gain and phase transfer function when measured at its Vout node:
(Click on image to enlarge)
But what happens when the component values vary over their tolerance range? Let's suppose that the resistors have 10% tolerance and the capacitors have 20% tolerance. Let's perform a Monte Carlo analysis on this circuit, given these tolerance values. The same circuit, but now set up with its Monte-Carlo functions and .param directives, looks like this:
(Click on image to enlarge)
(Note that within the "mc" function, I'm not setting the tolerance field to an actual number (although I could have done it this way, too). Instead, I'm using a separate directive (.param) to define the tolerances (in this case, 10% and 20%) globally.)
Running the Monte Carlo analysis 1000 times (via the directive ".step param run 1 1000 1") gives us the following spread of gain and phase plots:
(Click on image to enlarge)
But we can't be sure that we've truly evaluated worst-case performance. So let's instead use our new "worst-case" function for a worst-case evaluation.
The schematic, with its new Spice directives and functions, now looks like this:
(Click on image to enlarge)
And the analysis output, after 40 runs, looks like this:
(Click on image to enlarge)
Note the discrete intervals between plots. This is because the worst-case analysis is only using component values that are at the +/- tolerance limits for each component, and not any intermediary values (except for the first of the 40 plots, which uses the nominal component values for its analysis).
(Note: the above was edited on 29 May 2020 to replace two "worst-case" functions (wc_a and wc_b) with a single worst-case function, wc.)
Optimized Worst-case Analysis
(This section added 29 May 2020)
The worst-case analysis component values selected on a run-by-run basis for the simulations, above, are a function of random numbers. Therefore, to ensure that all combinations of "worst-case" component values have been evaluated, many runs need to be evaluated (above and beyond the "optimal" number of runs equal to 2^N, where N is the number of components being varied).
In the "Comments" section of this blog post, Harry Dymond (Electrical Energy Management Group, University of Bristol, UK) on November 9, 2012, posted an excellent technique for optimizing the number of runs necessary to perform a complete worst-case analysis.
If we consider, for worst case analysis, that each component has two possible values (nominal value plus tolerance, and nominal value minus tolerance), then these two value "states" can be represented by a single binary bit. In Harry's technique, "1" represents "nominal value plus tolerance", and "0" represents "nominal value minus tolerance.
Therefore, if we have N components in our circuit that we would like to vary the tolerances of, we can represent these components with N bits.
If we then stepped through all possible combinations of these N bits (from 0 to (2^N)-1), and at each step ran a simulation using the appropriate value of each component as defined by the state of its bit for that step, we would step through all possible combinations of the worst-case values without repeating or skipping a combination of values.
In other words, we would have optimized the number of runs to be the minimum set required for a complete worst-case analysis of our circuit
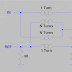
The table below demonstrates the component "bit" values for the 16 runs required for a complete worst-case analysis of 4 components:
Each component (that will be varied) is assigned a unique "Component Index" number. This index starts at 0 and increments by 1 for each component.
For example, if we are going to vary the tolerance of four components in a circuit, these four components are assigned index values starting with 0 for the first component, 1 for the next, 2 for the third, until we reach 3 for the fourth (and last) component.
You can think of these index values as each being a "bit position" in the N-bit word (where N, in this particular example, would be 4). For example, index 0 refers to the 2^0 bit location, index 1 refers to the 2^1 bit location, etc. You can see this in the table, above.
This table determines how the tolerances are set for each run. For Run = 0, all entries in the column for that run equal 0. Therefore, all four component values will have their tolerances subtracted from their nominal values.
For the next run, Run = 1, the component whose index is 0 will have its tolerance added to its nominal value. All other components will have their tolerances subtracted from their nominal values.
For the next run, Run = 2, now the component whose index is 1 will have its tolerance added to its nominal value. All other components will have their tolerances subtracted from their nominal values.
And for the next run, Run = 3, now the two components whose indexes are 0 and 1 will have their tolerances added to their nominal values. All other components will have their tolerances subtracted from their nominal values.
And so it goes, in a binary-counting fashion, until we reach the last run count of 15.
How do we do this using LTSpice? Here's the new schematic, using the same four components that we analyzed in our earlier, non-optimized worst-case analysis, above.
The differences between this new LTSpice simulation and the earlier version are:
1. The "wc()" function now has a third input variable: "index" (i.e. the "component index", and the function is now:
.function wc(nom,tola,index) if (run == -1, nom, if(binary_digit(run,index),nom*(1+tola),nom*(1-tola)))
2. The wc() function for each component (in each component's "value" field) is assigned a unique index. The index for the first component is 0, and indexes increment sequentially by 1.
3. The "binary_digit" function is a new function. It returns either a 1 or a 0, depending upon run-number and component index:
.function binary_digit(run,index) floor(run/(2**index))-2*floor(run/(2**(index+1)))
4. The "run" parameter now starts at -1 (as mentioned by "anonymous" on December 13, 2012, in the comments section, below). When "run" equals -1, the circuit simulation is run with nominal component values.
There are 4 indexes (and thus 4 bits) for this circuit. Thus, a complete worst-case simulation will require 16 runs to test all combinations of worst-case tolerances, plus there is one additional run with components set to their nominal values. So there are 17 runs, total.
OK, let's run the example!
First, here's the LTSpice schematic, again:
And here are the plots of the voltage at the "vout" node:
Please note that this technique (as described by Harry Dymond in his November 9, 2012 comment in my comments section below) is also described in the following article written by Linear Technology Corporation, in 2017:
https://www.embedded-computing.com/articles/getting-the-worst-case-circuit-analysis-with-a-minimal-number-of-ltspice-simulation-runs
(Note, too, that in my example, above, I've replaced Harry's use of "powerOfTwo" with the shorter word "index", used by the LTC authors.)
Other Notes and Caveats:
1. In the "comments" section, "Thomas", on December 2, 2016, points out that worst-case analysis could miss LC circuit resonances. If your circuit contains inductors and capacitors, Monte Carlo analysis (in lieu of Worst-case analysis) would probably be more appropriate.
2. Further information on Worst-Case and Temperature Analysis can be found here:
http://k6jca.blogspot.com/2012/07/worst-case-and-temperature-analysis.html
(And check out the other comments in the comments section, below, too).
Resources:
LTSpice is available for free from Linear Technology. You can find it here























31 comments:
Hi Jeff,
It's very helpful and just what I was looking for these days.
One question for you:
In the worst case analysis, you defined two functions for the resistor and capacitor respectively: wc_a() and wc_b(). But since their forms are the same, is one function wc_a() good enough for both resistor and capacitor?
Just a thought.
Thank you,
Sam
Hi Sam,
Thanks for the comment. I think you're right.
That is, you could define one "worst case" function, for example:
.function wc(nom,tol) if(run==1 ...(etc.))
and then for the component values use (wc(value1,tolb)}, {wc(value2,tola)},{wc(value3, tola)}, etc., where tola and tolb are defined in .param statements.
I'd want to try this first, but I can't think of any reason why it wouldn't work.
Thanks again!
- Jeff
I certainly enjoyed the way you explore your experience and knowledge about the subject.Thanks for this nice sharing keep posting more..
Hello Jeff,
Thanks for this blog post, I found it very useful. However, there are a couple of things that concern me:
1.) The built-in Monte-Carlo function "mc" uses a uniform probability distribution, rather than Gaussian. It's therefore probably better to use the following function for Monte-Carlo analysis:
.function normal(nom,tol) if(run==1, nom, nom*(1+gauss(tol/4)))
This uses a normal distribution and assumes manufacturer's quoted tolerance is based on a 4-sigma confidence (99.99% of shipped product will lie in quoted tolerance band).
2.) For the worst-case analysis, since the "wc" function randomly changes a component value, we cannot guarantee that all possible combinations of component values will be explored. You can bring the probability (that all possible combinations are explored) arbitrarily close to unity by increasing the number of simulation runs, but you can never make it actually unity! After some head-scratching I came up with the following functions:
.function binary_digit(x,powerOfTwo) floor(x/(2**powerOfTwo))-2*floor(x/(2**(powerOfTwo+1)))
.function wc(nom,tol,powerOfTwo) if(run==y, nom, if(binary_digit(run,powerOfTwo),nom*(1+tol),nom*(1-tol)))
Let's say you have 4 components that you wish to vary over their tolerance range. You require 2^4 + 1 runs (i.e., 17) to cover all the variations, plus 1 run with all values equal to their nominal. Set the number of runs as follows:
.step param run 0 16 1
Now, assign the values of the components as follows:
component 1: {wc(nominal_value,tolerance,0)}
component 2: {wc(nominal_value,tolerance,1)}
component 3: {wc(nominal_value,tolerance,2)}
component 4: {wc(nominal_value,tolerance,3)}
Finally, replace "y" in the "wc" function above with "16"
Now when you do your simulation run, you are guaranteed to have simulated all 16 different possible combinations of component value extremes exactly once each. Another benefit of this approach is that when looking at the results you can determine the actual component values used for a given result.
Enjoy!
Harry.
Thanks very much for your great comments, Harry!
Your reply raises an interesting question (for which I don't know the answer): are actual component values within a manufacturer's "Value" bins have a uniform or a Gaussian distribution? I suspect some (such as resistors) might have a uniform distribution, but I don't know. It probably depends upon the type of component and the manufacturing process.
Thanks again!
- Jeff
Jeff and Harry,
Thank you for this post and the comment. I found it very useful especially with the run-saving binary enhancement by Harry. I made one minor tweak for the binary count in "run": I started run at -1, and incremented by 1. This prevents the need to edit the wc() function every time the number of runs is changed. The nominal case is calculated when run==-1.
Jeff and Harry and all,
Thank you very much for this very interesting post.
Concerning your question Jeff, here is the answer :
On a process batch, all the resistors initially have a Gaussian distribution.
The manufacturer measures every resistance and sort them per tolerance.
This leads resistors to actually have a VERY strange distribution in the real world :
For a 100 Ohm resistor batch:
All the [99;101] Ohms resistors will be 1% resistors.
All the [95;99] and [101;105] resistors will be 5% resistors.
And so on.
This means that if you take a basket of 5% 100 Ohms resistances, you should never be able to find a 100 Ohm in it! In this basket, you'll get a gaussian distribution with a hole in the [99;101], and no "tails" in the distribution, since those resistors will belong to the 10% basket!
I found an article on that, and had a "holy sh.." moment when I understood how obvious yet bizarre that was.
I'll try to unburry it in all my stuff!
Hi,
really great post! Is x in the function: .function binary_digit(x,powerOfTwo) floor(x/(2**powerOfTwo))-2*floor(x/(2**(powerOfTwo+1))) equal to run?
Thanks
Sascha
Hi Sascha,
I believe the answer is yes.
If you look at Harry's equations, you'll see:
.function wc(nom,tol,powerOfTwo) if(run==y, nom, if(binary_digit(run,powerOfTwo),nom*(1+tol),nom*(1-tol)))
In this equation the variable run has been substituted for the x that we see used in the function definition: binary_digit().
- Jeff
Vey helpful, thanks a lot for the article and the comments.
Another point worth considering is that the tolerances given by the manufacturer apply to the product as it was shipped. Most circuits don't utilize resistors and capacitors hanging in the air, though. Therefore, the tolerances need to be widened based on expected change in value due to soldering-induced stresses. In my worst-case calculations, I double the resistor tolerance, and multiply the capacitor tolerance by 1.5 for NP0 and X7R and similar parts.
Yet another worthwhile point is to include the amplifier's GBW (really the 2nd open-loop pole) in the simulation. Depending on the sensitivity of the circuit to amplifier GBW, this may be important. GBW can vary wildly - by as much as factor of 2 or more.
Finally, if you expect variable output loading - say in an analog output exposed to the user - you should include at least the load extremes in the simulation. With good models, you should see effects of amplifier's AOL lowering under increasing load, and of the amplifier's output resistance.
Dear all,
Thank you for really great and useful posts.
However I have a simple question.
After mc or wc analysis how one can know what plot corresponds to which set of data (corner)?
Thanks,
P5K0
Hey there. Thanks for the awesome post. I tried using your example in DC but it always fails. I can't figure out why. Any suggestions?
That's an excellent question -- I usually use SPICE only for AC or Transient analysis, and so I've never tried it with DC. I'm traveling and out of town at the moment, but when I return home I'll check into it.
- Jeff
An update regarding LTSpice Monte Carlo analysis and DC, per the question above...
I created a simple voltage-divider circuit (components: one voltage source, two resistors) and gave each of these three components its own tolerance.
I then ran a 100-run Monte Carlo analysis on this circuit, looking at the voltage at the Voltage-Divider node.
Monte Carlo analysis ran fine using the Operating Point command (.op). It used all three tolerances.
Monte Carlo analysis ran with the DC Sweep command (.dc), in which the voltage source amplitude was swept, but in this case it did not use the tolerance I had assigned to the voltage source.
Monte Carlo analysis did not seem to work for the Transfer Function command (.tf).
Of course, the this last result might be due to an error on my part.
- Jeff
One more note regarding Monte Carlo analysis when running a DC Sweep...
As I mentioned in the previous comment, LTSpice ignores the "tolerance" assigned to the DC voltage source being swept.
BUT, if there are other voltage sources (with their own tolerances) in the circuit, the Monte Carlo analysis WILL vary these with each successive run, according to the tolerance values they've been assigned. (Note that this assignment is made in a component's VALUE field, e.g. the "mc(10K,tola)}" assigned as R1's value).
Hi,
is there any chance to read out any component values of a specific plot? Similar like it is possible with the .step param list function plots.
Cheers,
Chris
Hi Chris,
Unfortunately, I personally don't know of any way to link a specific plot to its component values. But that is not to say that there isn't a way...if there is one, however, I don't know it.
- Jeff
Thanks for your comment, Thomas. And I agree -- if you want to check for unanticipated resonances (or other forms of "local extrema") in a circuit, then Monte Carlo analysis would be a more appropriate method of analysis.
Best Regards,
- Jeff
Thank you very much for sharing this....
Hello Harry, Jeff,
Thanks for the great post. As I was trying to understand Harry's binary function:
function binary_digit(x,powerOfTwo) floor(x/(2**powerOfTwo))-2*floor(x/(2**(powerOfTwo+1)))I put it in excel and it was giving 0000 and 1111 alternatively for 4 components. I was expecting it to give 0000,0001,0010,..1111. Am I missing anything?
Thanks,
R
Hi R,
Thanks for the comment.
I just tested the binary_digit function in Excel, and it seems to work. Here is what I did:
Define cell A2 to contain the powerOfTwo value.
Define cells A4 to A19 to contain an integer count, increasing by 1 with each row, from 0 in cell A4 to 15 in cell A19.
In cell C4, define its contents to be:
=FLOOR(A4/(2^$A$2),1)-2*FLOOR(A4/(2^($A$2+1)),1)
And then copy this formula into cells C5 through C19. Note that the copy function should change the A4 in the formula to A5 when copied from cell C4 to cell C5, etc.
If you set powerOfTwo to be 0, you will see the values in column C alternating 0,1,0,1,0...etc.
If you set powerOfTwo to be 1, you will see the values in column C alternating 0,0, 1,1,0,0,1,1...etc.
If you set powerOfTwo to be 2, you will see the value in column C alternating 0,0,0,0,1,1,1,1,0,0,0,0,1,1,1,1.
and if you set powerOfTwo to be 3, you will see the values in column C alternating 0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1.
An important note to keep in mind: in Harry's comment above, each component's WC function has a *unique* powerOfTwo defined for it (it is the last value in the WC function's field). So, each component will be toggling between its max and min values at a different rate, according to the the appropriate power-of-two sequence (per the sequences I just listed, above) selected for it.
Hope this helps,
- Jeff
Excellent article, thanks for sharing. I have one point regarding tolerance distributions, although a single component may have a peculiar distribution as discussed in the comments, if you are simulating a circuit where several components vary, the central limit theorem means the end result should be close to Gaussian regardless so a uniform assumption per component is probably as good as any.
The problem I have is that the end result of a run is a display with a band results composed of many lines but the density makes no difference. Is there any way to turn this into a distribution to extract a mean and standard deviation for a parameter such as the gain or 3dB point in your example filter. Alternatively how about a histogram? I'm thinking maybe some way of exporting data points and processing in a spreadsheet would probably be needed.
Best regards,
George
Hi George,
That's a great question!
I personally don't know of a simple way to do it (usually I'm only interested in Min and Max values to ensure that a design meets specs).
From a quick Google search, it looks like one could download individual traces to individual text files and then import these files into, say, Excel for analysis. But I can see this becoming unwieldy for any significant number of traces.
Best regards,
- Jeff
Thanks for the response Jeff,
I use min/max to guarantee results but the mean +/- spread is used for "typical" figures so I'd like both.
I've been running typically 1000 to 3000 traces to get a reasonable density so I doubt that would be practical. Exporting one point per run calculated from the curve (e.g. for the 3dB point) would be possible but I haven't found how to export a value per run automatically.
Merry Christmas,
George
Thank you for posting this instructional. I found it very helpful and intuitive.
I've been using your method which i like because i am able to use the .step command additionally with for temperature. and is exactly what I need for reference on work I am doing. I am also comparing it this method below:
https://www.embedded-computing.com/articles/getting-the-worst-case-circuit-analysis-with-a-minimal-number-of-ltspice-simulation-runs
This method is similar but indexes the components to ensure all possible combinations. Via this method I can pinpoint which run/combination had the largest variance. But I am unable to identify those locations if I step the global temp parameter.
Does your method run through all possible combinations of min max tolerances for the components? Is the minimum number of runs the same as the method in the link to guarantee all possible combinations? Where can I identify the values of a particular run?
Thanks
Hi,
The Index method (described in the link you provided) should give the minimum number of runs necessary to do a worst-case analysis in which the tolerances of all components are varied.
The method I describe doesn't use Indexes, so it is a bit simpler. But, because the varying of component tolerances is random (rather than assigned via Indexes), there needs to be more runs to increase the probability that you've covered all cases.
I can't tell you how to identify the values of a particular run. You might want to address that question to Linear Technology.
- Jeff
Regarding how to determine component values for a particular run, I received the following email.
(Begin email quote...)
I notice a few people asking how you can work out the component values that have been used on a given monte-carlo simulation run. I discovered a clever idea in a comment by user “missperry” at this youtube clip:
https://www.youtube.com/watch?time_continue=694&v=KaGo9uxVgOg&feature=emb_logo
The comment is in reply to a comment by “Rowan Doherty”. The idea is to assign a value to both a component, and a voltage source, allowing the voltage source to be probed to read the value. He does somewhat over-complicate the idea by using two parameters where one will suffice (i.e., he could just have parameter “R” instead of “R” and “Vr”), but it’s a genius idea nonetheless. His .asc implementing the idea is available from here:
https://www.mediafire.com/folder/agdkb6p7167ox/Shared
(search for “RLC Monte Carlo.asc”)
(...end email quote)
- Jeff
Hello,
Thank you very much for the useful method for a "exhaustive" worstcase simulation.
Based on same smart principle of binary table I propose to short the functions to explore this table:
- same principle an index identify each components from 0.
example: R1 value is {wc(100, 1/100, 0)}
R2 value is {wc(100, 1/100, 1)}
- same principle writing the step directive for example ".step param run 0 16 1" for 4 component values.
- novelty is to create a single function ".function wc(nom,tol,index) nom*(1+tol*(-(run>0)**ceil(run/2**index)))"
the principle is based on the operation -1^x whose result switch between -1 and 1 in accordance with the exponent x is even or odd.
the values in the binary table become -1 and +1.
so the coefficient -1 and 1 is alternatly applied to the tolerances.
additionnaly "run>0" give 0 for run = 0, so this run calculate the nominal result, the following runs "run>0" = 1, with the minus we have the operation "-1^x" with x that depends on "run" and "index".
Thanks
Francis.
The correct number of runs to use is discussed here:
https://www.edn.com/monte-carlo-gone-wrong/
thank you
Post a Comment