SDR Notes: The Mixer Mathematics of Digital Down Conversion

(This post originally started as notes to myself, placed here so that I would not lose or forget them.)

The Digital Down Converter (DDC) is a basic block of FPGA-implemented SDR radios.  Per Wikipedia:

A digital down-converter (DDC) converts a digitized, band limited signal to a lower frequency signal at a lower sampling rate in order to simplify the subsequent radio stages. 

Below is an illustration of a DDC stage (don't worry about the math -- it will be explained later in this post):

(Click on image to enlarge)

Note that, for demonstration purposes, the equations assume a simple cosine as the input signal.

This post will look at the math involved in the Mixer.  I will leave the low-pass filter and sample-rate conversion for later posts.


First, some basics...

Basic Down-Conversion Mixing:

Historically, down-conversion has been done in the analog domain with a "real" oscillator signal (e.g. cos(ω_ot)).  Let's first look at this type of basic mixer before tackling mixing in the Digital (and Complex) domain.

For demonstration purposes, I'll simplify the receive-signal to be a just simple cosine signal at a single frequency:  cos(ω_it).

This mixer's math is straightforward.  Let the output of the mixer be y(t).

y(t) = cos(ω_it)*cos(ω_ot)

We can use Trigonometric identities to express this equation in terms of sums and differences of frequencies:

y(t) = (cos((ω_i−ω_o)t))/2 + (cos((ω_i+ω_o)t))/2

But this basic form of mixing has a problem if one would like to down-convert an incoming RF signal directly to base-band:  both the desired signal and its image will appear in the base-band spectrum (which, for the typical shortwave receiver, is the audio spectrum we want to hear).

This type of conversion is known as "Direct Conversion."  For an example, see Rick Campbell's R1 receiver.

Visually, here's how the frequencies shift, shown as a single-sided spectrum (which one would see if one did a "Trigonometric" Fourier Transform on the RF input.  Refer to equation 27 in this paper by Robert Marcus for more detail)::

Note the overlap of the two signals down at base-band...our "desired" signal would be interfered with by any signal at its "image" on the other-side of the oscillator's frequency!

And if we were to consider the Mixer's input to be a band of frequencies:

You can see the spectrum fold-back with the result being the desired signal and its undesired image occupying the same base-band frequencies.  A single-sided spectrum graph has no negative frequencies, and any "calculated" negative frequencies become positive frequencies via the Trig identity: cos(−ω_it) = cos(ω_it).

We can get around this image problem by working in the domain of Complex Numbers (numbers with a real and an imaginary component).  Specifically, we will use exponentials with complex arguments.


Complex Exponentials -- A Quick Review of Some Important Identities:

Euler's Formula:

e^jθ = cos(θ) + jsin(θ)

Similarly,

e^−jθ = cos(θ) - jsin(θ)

From Euler's Formula it can be shown that:

cos(θ) = (e^jθ + e^−jθ)/2

sin(θ) = j(e^−jθ − e^jθ)/2

Let's consider a real signal at a single frequency f_o (Hz), and let's express this signal simply as a cosine: cos(2πf_ot).

Using the identities above this signal can be expressed in exponential form:

cos(2πf_ot) = (e^j2πf_ot + e^−j2πf_ot)/2

Below is a representation, in the complex frequency-domain, of this signal :

(Source:  Quadrature Signals: Complex, but not Complicated, Richard Lyons)

And, for completeness, here are a two more illustrations:

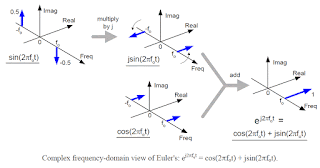
First, to complement the cosine representation above, here is a complex frequency-domain representation of a sine wave signal of the same frequency:

(Source:  Quadrature Signals: Complex, but not Complicated, Richard Lyons)

Second, we can use both of these illustrations of the signals in the complex frequency-domain to generate a visual representation of Euler's Formula, showing how the imaginary sine terms are rotated (when multiplied by j) to the real axis and then added to the real cosine terms:

(Click on image to enlarge)

(Source:  Quadrature Signals: Complex, but not Complicated, Richard Lyons)

Note that multiplying sin(2πf_ot) by j rotates the sine's complex frequency-domain imaginary components "clockwise" by 90 degrees to the real plane. If we were to instead multiply sin(2πf_ot) by -j, the rotation would be 90 degrees counter-clockwise, with the results again being on the real plane, but pointing in the opposite direction, and our final result (after adding the real components together) would represent Euler's Formula for a negative frequency, -f_o, instead of f_o.

Frequency Conversion using Complex Numbers in Exponential Form:

Let's use the above equations to shift signal frequencies.

First, for ease of demonstration, let's define an input RF signal, x(t), to be a simple cosine at a single frequency, f_i Hz.  I.e.:

 x(t) = cos(2πf_it)

To minimize my typing, I will express this signal's frequency as its radian equivalent, where ω_i = 2πf_i.

x(t) = cos(ω_it)

Using the identities above we can express cos(ω_it) as the sum of two complex exponential numbers:

cos(ω_it) = (e^jω_it + e^−jω_it)/2

Now let's now define our oscillator's signal as a complex exponential:

e^jω_ot

(Note that from Euler's Formula e^jω_ot  = cos(ω_ot) + jsin(ω_ot)).

Our next step is to multiply together the input signal and the oscillator signal.  We will call the output y(t).

y(t) =  cos(ω_it) * e^jω_ot

Replacing the input signal with its equivalent complex exponential form, the output equation becomes:

y(t) = [(e^jω_it + e^−jω_it)/2]*e^jω_ot

Finally, let's finish the multiplying.  The result is:

y(t) = (e^{j(ω_i+ω_o)t} + e^{j(−ω_i+ω_o)t})/2

Note that the frequency components in the arguments of both exponentials have been shift up by ω_o.

By the way, we can use Euler's Formula to express this result in terms of sines and cosines:

y(t) = [cos((ω_i+ω_o)t) + jsin((ω_i+ω_o)t)]/2 + [cos((-ω_i+ω_o)t) + jsin((-ω_i+ω_o)t)]/2

You can also derive the same result using only sines, cosines, and trigonometric identities and not complex exponentials, but the math is more cumbersome.


OK, so an NCO's output that is a complex-exponential with an argument whose frequency is +ω_o will shift the incoming signal's frequency up by ω_o.  What happens if the NCO's frequency is negative, i.e. -ω_o?

Using the same approach as above, the DDC's output can be shown to be:

y(t) = (e^{j(ω_i−ω_o)t} + e^{j(−ω_i−ω_o)t})/2

In other words, both of the input signal's complex exponentials are shifted down in frequency by ω_o. Voila, a Digital Mixer!

Again, note that y(t) can be expressed as the sum of sines and cosines.  Using the identities at the start of this post:

y(t) = [cos((ω_i-ω_o)t) + jsin((ω_i-ω_o)t)]/2 + [cos((ω_i+ω_o)t) - jsin((ω_i+ω_o)t)]/2

which is exactly equivalent to y(t) = (e^{j(ω_i−ω_o)t} + e^{j(−ω_i−ω_o)t})/2.


Mixing with Complex Exponentials:

With a view towards understanding SDR building blocks, let's look at a Digital Mixer using the down-conversion math I've just discussed, and which shifts signal frequencies in the digital (rather than analog) realm.

Below is a Digital Mixer block diagram using complex numbers.  Let's drive the RF input with a simple cosine signal, cos(ω_ot):

Note that the oscillator's output is a complex exponential with a negative frequency in its argument.  This negative frequency, as I've discussed earlier in this post, will down-convert incoming RF.

The input signals' spectrum (shown below as two-sided, with negative frequencies, per the frequencies in the complex arguments in the exponential form of the input signal) will shift down:

(Click on image to enlarge)

The illustration below shows a more general case for a band of frequencies at the DDC's input:

(Click on image to enlarge)

Note that, unlike the analog mixer described at the start of this post, this spectrum has both positive and negative frequencies.  In other words, we do not (yet) have an issue with "image wrapping" while we remain in the complex domain.

Another take on the same topic, from "Complex Signal Processing is Not -- Complex," by Ken Martin, showing the same:

(Source: "Complex Signal Processing is Not -- Complex,",Ken Martin)

Note (again) that the input consists of only real, not complex, numbers, but the output Y(t) will be in complex form, with both real and imaginary components.

Regarding the mixer (c) in the image above, we can express its two outputs (y_r(t) and y_q(t)) in terms of sines and cosines.

First, for simplicity of analysis let's define the input x_r(t) to be a simple cosine at frequency ω_r:

x(t) = cos(ω_rt)

Noting that the oscillator frequency is ω_i in this example, the output y_r(t) is therefore:

y_r(t) = cos(ω_rt)*cos(ω_it)

which, using trig identities, expands to:

y_r(t) = cos((ω_r−ω_i)t)/2 + cos((ω_r+ω_i)t)/2

Now let's do the same to derive y_q(t), the imaginary term...noting that −sin(ω_it) = sin(−ω_it), y_q(t) becomes:

y_q(t) = sin((ω_r−ω_i)t)/2 − sin((ω_r+ω_i)t)/2

Is this result equivalent to the result derived (above) using complex-exponential equations?

Essentially, yes it is!

Let's multiply the y_q(t) channel by j (i.e. add a phase shift of 90 degrees with, say, a Hilbert Transform) and call this output y_q(t)' (note the 'prime').  Its equation is:

y_q(t)' = jsin((ω_r−ω_i)t)/2 − jsin((ω_r+ω_i)t)/2

If we then add y_r(t) and y_q(t)', the result is:

y_r(t) + y_q(t)' = [cos((ω_r−ω_i)t) + jsin((ω_r−ω_i)t)]/2 + [cos((ω_r+ω_i)t) − jsin((ω_r+ω_i)t)]/2

Which, from Euler's Formula, we know is exactly equivalent to:

y_r(t) + y_q(t)' = (e^{j(ω_r−ω_i)t} + e^{j(−ω_r−ω_i)t})/2.

and which is exactly equivalent in form to the equation we derived earlier:

y(t) = (e^{j(ω_i−ω_o)t} + e^{j(−ω_i−ω_o)t})/2

In other words, the trigonometric signals representing y_r(t) and y_q(t) are the fundamental mathematical elements (when the sine terms are multiplied by j) that constitute the Digital Mixer's operation when expressed in complex-exponential form.

Links and Other Resources:

An Excellent Tutorial on Complex Numbers:  Quadrature Signals: Complex, but not Complicated, Richard Lyons

An interesting site to surf:
https://www.dsprelated.com/freebooks/mdft/Positive_Negative_Frequencies.html

Representing a signal as the sum of two exponentials:  http://ece.mst.edu/media/academic/ece/documents/classexp/ee216labs/EE216_Lab4.pdf

The Significance of Negative Frequencies in Spectrum Analysis, Robert Marcus, IEEE Transactions on Electromagnetic Compatibility, Dec. 1967.  (A copy can be found here).

Good tutorial on Complex Number in Radio applications:  Complex Signal Processing is Not -- Complex, Ken Martin

Standard Caveat:

I could have easily made a mistake in any of the above text, equations, or drawings.  If something looks wrong or is confusing, please feel free to contact me.  Thanks!