Notes on Directional Couplers for HF

Many years ago, when I was a student studying Electrical Engineering, one of my professors mentioned that the Standing-Wave Ratio (SWR) on a transmission line could be calculated by first finding (and measuring) a voltage maximum on a transmission line and then moving 1/4 wavelength away and measuring the voltage there.  If there were a standing wave, there would be a voltage minimum at this point.  And these two values (voltage maxima and minima) could then be used to calculate the standing wave ratio:

SWR = |Vmax| / |Vmin|

And I remember thinking...the inexpensive Radio Shack SWR meter that, as a teenager, I'd been using with my ham radio was only about 5 inches long.  Nowhere near the 20 meters (65 feet) of length required if SWR were to be measured on 80 meters the traditional maxima/minima way.  How did it work?  Something else must be going on inside those meters, but what?

Wait a sec...to measure SWR on 80 meters,

shouldn't these connectors be 65 feet apart?

Many years later, I finally decided to dig a little deeper...

On HF, SWR is measured using "lumped-element" directional couplers.  By "lumped-element" I mean that the components of the coupler and their interconnections are all much much shorter than the wavelengths of the frequencies being measured.

There seem to be two main topologies for these lumped-element couplers.  I'll call these two topologies the 1) Tandem  coupler (or bridge), and the 2) Bruene coupler, or bridge (after Warren Bruene, of Collins Radio).

The Tandem coupler topology was popularized for ham radio use by John Grebenkemper in his article, "The Tandem Match -- an Accurate Directional Wattmeter", which appeared in the January, 1987 issue of QST magazine.

(QRPers might recognize this as the "Stockton" bridge, named after David Stockton, G4ZNQ, for his article "A Bi-directional Inline Wattmeter," in the Winter 1989/90 issue of Sprat.)

The Bruene directional coupler is an older design, and it made its first appearance (to my knowledge) in Bruene's article "An Inside Picture of Directional Wattmeters," in the April, 1959 issue of QST.

Here's an example of the Bruene directional coupler:

Being lumped-element couplers, both of these designs operate by sampling the line voltage and line current at a single point (not two points 1/4-lambda apart!).  Both sample the line current with a transformer.  Their difference is how they sample line voltage -- line voltage is sampled with a second transformer in the Tandem coupler, while Bruene uses a capacitive divider to sample this voltage.

In other words, although the two topologies appear different, their fundamental principles of operation are essentially the same.

Let's get a better understanding of how these couplers (or bridges) operate.  I'll focus on the Tandem Coupler:

The "Tandem" Directional Coupler, in a Transmission Line Environment

Before getting into the discussion of the Tandem Coupler in an environment with Forward and Reflected waves, let me make an important point:

The Tandem Coupler, being made of "lumped elements" (in this case, two toroidal transformers and two resistors), is only looking at the voltage and current present at its output port.  It has no idea what the load is, or even how the load is connected to the port.  The load might be a resistor or other component simply clipped onto the output connector with test leads, or it might be a length of transmission line with a load (either known or unknown) at its other end.

Irrespective of what the load is (transmission line, clipped-on component, or whatever), the Tandem Coupler gives us voltage readings that can be interpreted in terms of Forward and Reflected waves.  It is important to remember:  these readings should only be interpreted as representing actual Forward and Reflected waves when the Tandem Coupler is connected in a transmission line with the same characteristic impedance, Zo, as the Tandem Coupler's designed-for target impedance!

Therefore, for this discussion I will assume that the Directional Coupler is inserted into a transmission line of the designed-for (target) characteristic impedance.

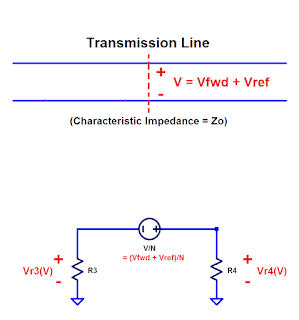
 Tandem Directional Coupler (W1QG)

Let's consider a transmission line with two independent signals on it.  One signal (let's call it the Forward signal) is traveling left-to-right on the line, while other signal (let's call it the Reflected signal) is traveling right-to-left.

These signals have voltage amplitudes of Vfwd and Vref, and, because they are independent of one another, their currents Ifwd and Iref are simply the signal voltages divided by the characteristic impedance of the transmission line.  That is:

Ifwd = Vfwd/Zo

and

Iref = Vref/Zo

From the Principle of Superposition, we know that V at any point on the transmission line is simply Vfwd+Vref.  And the total current at any point on the line, I, is equal to Ifwd - Iref (they subtract because the currents flow in opposite directions).

So now let's insert the tandem coupler into the transmission line at that point, as shown in the drawing below.  Note that I'm simplifying the drawing and not including source or load impedances (at either end of the transmission line) for this analysis.   

So what's going on inside the directional coupler?

First, note that the total current, I, flows through L1.  Therefore the current through L2 is I/N, or (Ifwd-Iref)/N, where N is  the turns ratio.

Similarly, the total voltage across L3 is V.  Therefore, the voltage across L4 is V/N, or (Vfwd+Vref)/N.

To see this, first let's define the orientations of the primary and secondary voltages and currents in each transformer, given the "polarity dots" of their windings:

Next, let's assign values to these voltages and currents based upon the transmission line's forward and reflected voltages and currents:

The measurement ports for this device are across R3 and R4.  So let's calculate the voltages across these two resistors.

For simplification of the calculations, I am going to assume the following:

1. The voltage drop across L1 is negligible.
2. The current through L3 is negligible.  

To demonstrate how this coupler works, I am going to assume that the two transformers are ideal transformers.  Also, I would like to use the Principle of Superposition to calculate the voltages across R3 and R4.  But to use this technique, I need to somehow model the transformers as independent voltage or current sources.

Typically an ideal transformer can be modeled as two dependent sources:

I will use the circuit on the left to model the voltage-sensing transformer (with the voltage source's value changed to V1/n, because the 1-turn winding is the secondary of the voltage-sensing transformer).  And I will use the circuit on the right to model the current-sensing transformer.  But I need to convert each two-dependent source model to one-independent source model.

Let's start with this model showing the Tandem Match's two transformers each replaced with two dependent sources:

The first step -- if I assume that the dependent current source representing the primary of the voltage-sensing transformer introduces negligible current into the transmission line (compared with the current on the line if the Tandem Match were not inserted into the line), then I can replace this source with an open (i.e. representing 0 current).

(Note:  Given that the transmission line's current at the point of measurement due to the load's impedance at that point equals V/Zload', where V is the voltage across the transmission line and Zload' is the load impedance as measured at that point, and given that the current added to the transmission line by the voltage-sense transformer model's dependent current source is V/(2*Zo*(N^2)), then the dependent current source has negligible effect on the transmission line's current if 2*Zo*(N^2) >> Zload'.  (I'll derive this equation later in the post).)

And if I assume that the dependent voltage source representing the primary of the current-sensing transformer introduces a negligible voltage drop into the transmission line (compared to the voltage across the transmission line at the point of measurement if the Tandem Match were not inserted into the line), then I can replace this source with a short (i.e. representing 0 volts).

(Note:  And given that the transmission line's voltage at the point of measurement due to the load's impedance at that point equals I*Zload', where I is the transmission line's current and Zload' is the load impedance as measured at that point, and given that the voltage added into the transmission line  (in series with the load) by the current-sense transformer model's dependent voltage source is I*Zo/(2*N^2), then the dependent voltage source has negligible effect on the transmission line's voltage if Zo/(2N^2) << Zload'.  (I'll derive this equation later in the post).)

The figure below shows the two new models:

(Note that the voltage-sensing transformer's model now represents the correct n:1 turns ratio).

The transformers have now been converted to models each containing a single dependent source.  To convert these two dependent sources to independent sources, recognize that in this application, if these dependent sources have negligible impact on  the current or voltage upon which either depends, then neither affects the other, and thus, for all intents and purposes, these two sources are essentially independent sources, and I can proceed with my analysis using the Principle of Superposition.

I will replace the L1/L2 transformer with a current-source and the L3/L4 transformer with a voltage-source, like this:

To calculate the voltages across R3 and R4, I'm going to use the Principle of Superposition and first calculate the contribution of the voltage-source to the voltages across these two resistors (with the current-source replaced with an open circuit, per the Principle of Superposition.

I will then calculate the contribution of the current-source to the voltages across these two resistors, with the voltage-source replaced with a short.

Let's start with the contribution of the voltage-source to the voltages across R3 and R4.  In the figure below I've replaced the current source with an open circuit and I've defined the voltage polarities across R3 and R4.

Before starting this calculation, let's first assume that R3 = R4 (which, in fact, they do).

Thus, the voltage of the voltage-source is equally divided between the two resistors.  So, the "V" contribution to Vr4 is:

Vr4(V) = (Vfwd+Vref)/(2*N)

Similarly, the "V" contribution to Vr3 is:

Vr3(V) = -(Vfwd+Vref)/(2*N)

Note:

1. Vr3's minus sign is because the actual polarity is opposite of the polarity I arbitrarily defined in the picture above.
2. The factor of 2 is because the voltage across each resistor is 1/2 of the voltage-source's value.

Now, let's calculate the contribution of the current-source, "I", to the voltages across R3 and R4.  Per the Principle of Superposition, I first must replace the voltage source with a short, as shown below:

Because R3 = R4, the current divides equally between  the two resistors, and the voltage across each resistor, due to "I", is:

Vr3(I) = -R3*(Ifwd-Iref)/(2*N)

Vr4(I) = -R4*(Ifwd-Iref)/(2*N)

I can now calculate the total voltage across each resistor which, because of the Principle of Superposition, is the sum of the voltages I've just calculated.  Starting with Vr3:

Vr3 = Vr3(V) + Vr3(I)

Substituting, we get:

Vr3 = -(Vfwd+Vref)/(2*N) - R3*(Ifwd-Iref)/(2*N)   (equation 1)

We can do the same for Vr4.  The result is:

Vr4 = (Vfwd+Vref)/(2*N) - R4*(Ifwd-Iref)/(2*N)    (equation 2)

[Sidebar:  Note that equations 1 and 2 allow us to express Vr3 and Vr4 in terms of the line V and I (where V = Va+Vb and I = Ia-Ib, as we defined earlier in this post).  

Vr3 = - (V + I*R3)/(2*N)    (equation 1a)

Vr4 =   (V - I*R4)/(2*N)    (equation 2a)

In other words, Vr3 is an expression in which the voltage-sample and current-sample voltages are summed, while Vr4 is an expression in which the voltage-sample and the current-sample voltages are differenced.]

OK, let's get back to simplifying equations 1 and 2...

Recall that:

Ifwd = Vfwd / Zo

and

Iref = Vref / Zo

where Zo is the characteristic impedance of the transmission line.

If I substitute these into equations 1 and 2, the equations become:

Vr3 = [Vref*(R3 - Zo) - Vfwd*(R3 + Zo)] / (2*Zo*N)

and

 Vr4 = [Vfwd*(Zo - R4) + Vref*(Zo + R4)] / (2*Zo*N)

Still pretty complex.  But we can simplify even further...

We've already defined R3 to be the same value as R4.  Let's also define these values to be the same resistance as the characteristic impedance, Zo, of the transmission line (for example, they could be 50 ohms, if the transmission line were 50 ohm coax).  That is:

R3 = R4 = Zo

This is an important equality.  If R3 and R4 don't equal Zo, the Tandem Match circuit will not correctly calculate forward and reflected voltages.

Substituting this equality into our two equations, the equations reduce to:

Vr3 = -Vfwd/N            (equation 3)

and

Vr4 = Vref/N            (equation 4)

In other words, selecting R3 and R4 to equal Zo (and assuming the voltage drop across L1 and the current through L3 are both negligible), then:

1. The voltage across Vr3 is solely a function of Vfwd (the signal moving from left-to-right on the transmission line).
2. The voltage across Vr4 is solely a function of Vref (the signal moving from right-to-left on the transmission line).

Note:  By measuring Vr3 and Vr4, we now know the voltages Vfwd and Vref.  Thus, we also know Forward and Reverse Power:

P(forward) = Pa = (Vfwd^2))/Zo = (Vr3^2)*(N^2)/Zo

P(reverse) = Pb = (Vref^2)/Zo = (Vr4^2)*(N^2)/Zo

Calculating the effect of the dependent voltage and current sources on Transmission Line voltage and current:

The transformers in the Tandem Match each be modeled as two dependent sources:

Earlier in this post I mentioned that if we assume that the two-dependent source models for our transformers have negligible impact upon the transmission line current and voltage, then we can model each transformer as a circuit containing one independent source.

Let's calculate when this assumption is true.  First, let's define the voltage polarities and the current directions based upon the voltage polarities and current directions defined for the transformers:

Therefore, the current-sense transformer's voltage polarities are:

Recognize that the voltage across the secondary of the current sense transformer (with the voltage-sense transformer removed from the circuit) is simply the current of the model's independent current source times R3 and R4 in parallel, which, because R3 = R4 = Zo, means that the secondary voltage is (I/N)*(Zo/2), which can be expressed as I*Zo/(2N).

If the secondary voltage is I*Zo/(2N), then the primary voltage is simply this value divided by N (because it is a 1:N transformer).

Therefore the voltage inserted by the current-sense transformer's primary into the transmission line is:

Vpri = Vsec/N = I*Zo/(2*N^2)

The voltage across the Zload' (the load impedance seen by the transmission line at the point of measurement, assuming Vpri is negligible) is I*Zload'

Therefore, I can state that Vpri is negligible if I*Zo/(2*N^2) is significantly smaller than I*Zload'.  In other words, for  the assumption to be true, the following condition must be met: Zo/(2*N^2) << Zload'.

Next, the voltage-sense transformer (current directions as defined in the transformer circuit, above):

For the voltage-sense transformer, the current added to the transmission line's current by the dependent current source representing the voltage-sense transformer's n-turn primary winding (i.e. Ipri) is the secondary's current divided by N:

Ipri = Isec/N

Isec can be shown to be (if we ignore the effect of the current-sense transformer) (V/N)/(2*Zo), given that R3 in series with R4 are the load of the voltage-source representing the transformer's secondary (ignoring the current-sense transformer). And, because R3 = R4 = Zo and the voltage source representing the secondary has a value of V/N, where V is the transmission line's voltage at the point of measurement.

Therefore:

Ipri = Isec/N = V/(2*Zo*(N^2))

The transmission line's current, if we assume the effect of Ipri is negligible, equals V/Zload'.

Therefore, Ipri is negligible compared to the transmission line's I if V/Zload' is significantly greater than V/(2*Zo*(N^2)), which is met if (2*Zo*(N^2)) >> Zload'.

Analyzing the "Tandem" Directional Coupler in a "Non-Transmission Line" Environment

As stated earlier, this coupler is actually a "lumped-element" device.  That is it's really looking at the voltage and current relationship at, essentially, a single point on the transmission line.  And we can therefore analyze it as a "lumped-element" circuit.  That is, we can analyze its operation as a circuit consisting of a combination of transformers, L's, C's and R's, and no transmission lines or traveling waves.

The drawing below illustrates this concept.  Zload is the load at the coupler's output port.  Let's assume the connection between the coupler and Zload is very short with respect to the wavelength of the signal being measured (it isn't a transmission line):

Note that I haven't shown a driving voltage-source (nor the source-impedance of this source).  It's actually there, connected to the left-hand IN port.  But all I care about is the voltage level, V, at the IN port.


Let's again simplify the analysis by first assuming that the voltage drop across L1 and the current through L3 are both negligible.

Clearly, if there is no voltage drop across L1, then the voltage across Zload is the same as the voltage at the IN port and across L3's N turns.  Let's call this voltage V.
And therefore current I through L1 is simply:

I = V / Zload.

Because L1/L2 and L3/L4 are both transformers, the current through L2 is I/N, and the voltage across L4 is V/N.

We can substitute ideal current and voltage sources for the two transformers (as we did before), and the circuit now looks like:

Using the Principle of Superposition, we can separately analyze the contributions of the voltage source and the current source to Vr3 and Vr4 and then sum these contributions together.

Doing this, we get:

Vr3 = -V/(2*N) - (I*R3)/(2*N)       (equation A)

and

Vr4 = V/(2*N) - (I*R4)/(2*N)        (equation B)

Let's express these in terms of V.  To do this, first recognize that:

I  = V / Zload

Using this relationship, we get:

Vr3 = -V*(R3 + Zload) / (2*N*Zload)      (equation C)

and

Vr4 = V*(Zload - R4) / (2*N*Zload)       (equation D)

Note that V is an unknown, so let's eliminate it from our equations.  To do this, let's rearrange equation C:

V / (2*N*Zload) = -Vr3 / (R3 + Zload)

Substituting this into equation D, we get:

Vr4 = -Vr3*(Zload - R4) / (Zload + R3)   (equation E)

Well, this is interesting.  Note the term:

(Zload - R4) / (Zload + R3) 

Let's say we've designed the coupler for use in a system with a Zo of 50 ohms. So R3 and R4 should be selected to equal the Zo of 50 ohms, and thus:

Vr4 = -Vr3 * (Zload - 50) / (Zload + 50)   (equation F)

(If Vr4 is negative it just means that it is 180 degrees out of phase from Vr3.)

Note the term:

(Zload - 50) / (Zload + 50)

This is the definition of the Reflection Coefficient, Γ (in which 50 is Zo, the characteristic impedance of a transmission line system that this directional coupler might be used in):

Γ = (Zload - Zo) / (Zload + Zo)  

And therefore:

 Γ = -Vr4 / Vr3    (equation G)

So, in other words, if we normalize Vr4 with respect to Vr3, the resulting voltage equals the Reflection Coefficient!

If you are familiar with the inexpensive SWR meters used for Amateur Radio, this is essentially what they do.  You are normalizing the magnitude of Vr4 with respect to the magnitude of Vr3 when you adjust Vr3 to deflect the SWR meter to full-scale before flipping the switch to measure Vr4.  When you do this:

• Full-scale meter deflection equals a |Γ| of 1.
• Zero meter deflection equals a |Γ| of 0.
• And a mid-scale meter deflection equals a  |Γ| of 0.5

(Note:  the SWR Meter is only using the magnitude of Gamma (the magnitude of Gamma is also known as rho).  There is no angle information.)

How does |Γ| relate to SWR?

SWR = (1+|Γ|) / (1-|Γ|)

So if we know the magnitude of Γ (and we do), we therefore know SWR from the above formula.

Remember that the meter, when set to measure Vr4, measures |Γ| over the range from 0 to 1 when the meter is first adjusted to have Vr3 drive it to Full Scale.  We can create an alternate scale, using the above equation, to give us SWR.

|Γ|    SWR

    0     1.00 

 0.1     1.22

 0.2     1.50

 0.3     1.86

 0.4     2.33

 0.5     3.00

 0.6     4.00

 0.7     5.67

 0.8     9.00

 0.9   10.00

 1.0   infinite

Note, for example, that 50% of Full-scale (|Γ| = 0.5) represents an SWR of 3.

Here's a meter and scale I found on the internet (from PY2OHH).  You can see that its SWR markings follow the table above.  E.g. SWR of 3:1 is 50% of the meter's FS.

Summing up:

From the above discussion, it should be evident that we don't need to use concepts of Forward and Reflected waves to understand how the Tandem Match coupler (and SWR meters based on it) operate.

Our typical SWR meter is really just calculating a relationship between the load at its output port (Zload) and its own terminating resistors, R3 and R4.  And this relationship is equivalent to the Reflection Coefficient if R3 and R4 have the same value as Zo of a Transmission Line.

Zload could be a load connected directly to the coupler's "OUT" port with a couple of wires, or it could be the impedance "presented" to the port by a long length of transmission line (an impedance determined, at that point, by the interaction of the Forward and Reflected waves).

The coupler doesn't care "how" the load is connected to its OUT port.  It's just looking at the relation between the voltage across the OUT port and the current through the OUT port.  It doesn't know anything else about the load except for this voltage and current relationship at its OUT port.  For example, if the OUT port happens to be connected to a transmission line, the coupler has no knowledge of the line's Zo. It doesn't even know if there's a transmission line attached, nor that the impedance it sees at its OUT port might be due to the interaction of Forward and Reflected waves.

For this reason, never assume that the meter reading is the actual Reflection Coefficient, Γ, or that the SWR reading is the actual SWR reading of the line.  It might not be.  We are really just measuring the relationship between Zload (as it appears at the OUT port) and the values of R3 and R4.  Only if R3 and R4 equal the actual characteristic impedance, Zo, of the transmission line would we truly be measuring the Reflection Coefficient.


Continuing on...

Here's something else we could do with Vr3 and Vr4:  if we know Vr3 and Vr4, we could also solve for Zload, our unknown load.  Here's how...

Let R3 = R4 = Rt, where Rt is the value we select for our termination resistors at the FWD and REF ports (they could be equal to Zo, but they could be anything else, too.  It only matters that R3 = R4).

Substituting and solving equation E for Zload:

Zload = Rt *(Vr3-Vr4) / (Vr3+Vr4)    (equation H)

Note that these variables and voltages represent complex numbers -- they have both magnitude and phase.  

The above analysis assumes Vsource and Rsource are unknown (often the case if discussing radio transmitters).  But suppose they are known (e.g. if you're using a signal generator).  We can do a similar analysis:

Lumped-element analysis for a known Vsource and Rsource:

Suppose Vsource and Rsource are known (for example, suppose we are using a signal generator with a known 50 ohm source impedance and a known signal level).  Let's rewrite the equations for Vr3 and Vr4 in terms of these new values.  First, we know that

I = Vsource / (Rsource + Zload).

V =  Vsource * (Zload) / (Rsource + Zload).

Substituting these two equations into Equation A and B from above and solving, we get:

Vr3 = -Vsource*(Zload + R3) / (2*N*(Zload + Rsource))

and

Vr4 = Vsource*(Zload - R4) / (2*N*(Zload + Rsource))

If Rsource = R3 = R4, these two equations simplify to:

Vr3 = -Vsource / (2*N)   (equation 3)

and

Vr4 = Vsource*(Zload - Rsource) / (2*N*(Zload + Rsource))   (equation 4)

What do these two equations tell us?

Vr3 will be constant, independent of load.  That is, Vr3 is solely a function of Vsource.

And, because Γ = (Zload - Zsource) / (Zload+Zsource)  [Note -- this is per Wikipedia.  I prefer to use Zo in lieu of Zsource, but if we assume Zo = Zsource, then they are equivalent.].

Vr4 = Γ*(Vsource / (2*N))

 
So Vr4 is directly proportional to a transmission line system's Reflection Coefficient.  Not surprising.  And if we substitute Vsource = -Vr3 * (2*N) (from equation 3) into the equation for Vr4, then

Vr4 = Γ * (-Vr3)

or

Γ = -Vr4 / Vr3

Which is the same as equation G from our first lumped-element analysis. 

Links to my Directional Coupler blog posts:

Notes on the Bruene Coupler, Part 2

Notes on the Bruene Coupler, Part 1

Notes on HF Directional Couplers (Tandem Match)

Building an HF Directional Coupler

Notes on the Bird Wattmeter

Notes on the Monimatch

Notes on the Twin-lead "Twin-Lamp" SWR Indicator

Calculating Flux Density in Tandem-Match Transformers


And some related links from my Auto-Tuner posts:

Auto Tuner, Part 5:  Directional Coupler Design

Auto Tuner, Part 6:  Notes on Match Detection

Auto Tuner, Part 8:  The Build, Phase 2 (Integration of Match Detection)

HF PA, Part 5: T/R Switching and Output Directional Coupler


Links and Articles for Further Reading:

• Explanation of the Bruene Coupler

• N2PK Power and Return Loss Meter (PDF) -- good article and discussion of Bruene vs. Tandem Couplers

• N2PK Power and Return Loss Meter (web page)

• Ellis -- RF Directional Coupler

• The Tandem Match -- A Closer Look 

• LP-100 Wattmeter -- QEX article by N8LP that contains a good discussion on directional coupler design.

• If you can access the ARRL's site for QST back issues, you can also look up Bruene's April, 1959 article and Grebenkemper's January, 1987 article (and further Tandem match discussion in January, 1988, and July 1993).

• US Patent 2285211, Korman, Radio Frequency Wattmeter, Granted June 2, 1942.  Similar to the Tandem Match coupler

Other notes...

1.  A note from Dick Benson, W1QG: 

One sad, but true, reality is to make one of these work well takes more than the usual amount of black magic.

Strays are everything.   The VNA is indispensable in maximizing performance.  

(VNA = Vector Network Analyzer.  E.g. HP 8505, 8753, 3577, etc.)


2.  3/28/2019.  The comment below was made to a different post in this blog.  I thought it worthwhile to add it here.)

Good day Jeffrey, 

I recently visited your site on this coupler. I was in the process of presenting a class on reflection coefficient measure and decided to build a coupler for lab work for the students. Accomplished at low frequencies, 1 MHz-30 MHz, it is straight forward to obtain a sufficient Vinc and Vrefl voltage to operate and trigger a low cost scope. 


As you present in your documentation, the value of GAMMA is the NEGATION of the usual GAMMA definition. Surprise comes about when you attempt to explain the NORMAL action of the reflected voltage across a short, It should be 180 degrees out of phase with the incident voltage so NO voltage is present across the short. An open circuit is exactly opposite and Vinc should be in phase with Vref. However, for both cases it is the exact opposite for this coupler. 

I think this would be a worthwhile item to mention in the blog, particularly when one decides to build the coupler and actually go in there and measure the PHASE of the voltages; Vrefl and Vinc. A bit of head scratching at first! 

Thanks, Alan Victor, W4AMV

This is a good point: the circuit topology as described above results in Vfwd being proportional to -Vr3 (per the mathematical derivation), rather than +Vr3.  I will note that if it is important to the user that Vfwd be the same polarity as Vr3, this could probably be accomplished by changing the phase of one of the transformer windings (I will leave the analysis to the reader).  

Caveats:

These notes are meant to aid the reader in understanding how directional couplers work.  But this is not a rigorous analysis.  I've made a number of assumptions to simplify the math.  For example, the two transformers within the Tandem Match coupler are assumed to be ideal.  In the real world, they are not.  A complete analysis would take into account, for example, their inductances and the mutual coupling between primaries and secondaries.

Finally, I could easily have made a mistake in my interpretations and/or analysis.  So take everything with a grain of salt.  If there's something here that doesn't look right to you, please feel free to email me.