In this blog post I will derive equations representing a transmission line of characteristic impedance Zo and of length 'l' as a two-port network. As a result, there will be a total of four different pairs of equations, each pair representing the two-port network in a different way.
These pairs of equation will be:
1. V and I at Port 2, in terms of V and I at Port 1, for a lossy transmission line.
2. V and I at Port 1, in terms of V and I at Port 2, for a lossy transmission line.
3. V and I at Port 2, in terms of V and I at Port 1, for a lossless transmission line.
4. V and I at Port 1, in terms of V and I at Port 2, for a lossless transmission line.
(These last two sets of equations are special cases of the first two sets).
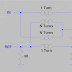
The image below shows these voltages and currents for both the transmission line and its two-port model.
We can also express the forward and reverse voltages at either end of the transmission line as functions of the Total Voltage and Current at either end:
I will use equations 1, 2, 3, and 4 (in the figure, above) to derive the two-port network equations, but before I go any further in this derivation, let me first define a transmission line's "Propagation Constant."
Sidebar on the exponential terms e-γl and eγl :
Assuming a sinusoidal signal on the transmission line, the exponential term e-γl (or eγl) represents the effect on a sine wave's amplitude and phase, due to the transmission line's Propagation Constant, γ, as that wave travels along the transmission line.
The other variable in the exponent is 'l', which represents the length that the wave has traveled (or will travel) along the transmission line.
The Propagation Constant is a complex number: γ = α + jβ, where α represents a "real" change in signal amplitude (either positive or negative, i.e. attenuation or gain), and jβ represents a phase shift of the sinusoidal signal, either a positive phase shift or a negative phase shift.
Both of these values are in terms of unit-length, and so when substituted into the exponential, multiplying α by the length of the line gives overall attenuation (or gain, depending upon reference point), and multiplying jβ by length gives phase-shift for the wave's journey along a defined length of line.
If we were to take a snapshot in time and simultaneously compare the Forward Voltage V+ at point 1 with the Forward Voltage V+ at point 2, we would see that the voltage at point 2 has a negative phase shift compared to the phase of V+ at point 1, because the voltage at point 2 represents an earlier version of V+ that had been at point 1 at an earlier point in time, compared to the V+ that is currently at Point 1.
We would also see that the amplitude of V+ at point 2 has been attenuated relative to its original amplitude at point 1 due to transmission line loss as it traveled from left to right along the line. Thus, γ's "α" term (in the Propagation Constant's equation γ = α + jβ) is negative to represent this loss at point 2 compared to the amplitude at point 1.
The figure below demonstrates both the attenuation and the phase shift at point 2, compared to point 1, for the Forward moving voltage wave:
The figure below demonstrates both the amplitude and phase at point 2, compared to point 1, for the Reverse moving voltage wave.:
With this information and the equations, above, we can derive network equations that represent a lossy transmission line of length 'l'.
Lossy Transmission Line Equations for V2 and I2 in terms of V1 and I1:
From the previous two figures that describe phase-shift and attenuation of V+ and V- at Point 2 compared to our reference at Point 1, we can create the identities represented by equations 5 and 6 in the figure, below, and, using these, represent V2 as a function of Point 1's V+ and V- :
The matrix form of these last two equations is:
Lossy Transmission Line Equations for V1 and I1 in terms of V2 and I2:
This time, we begin by considering the Forward Voltage V+ and the Reverse Voltage V- from Point 2 (rather than from Point 1, as we did for the first derivations).
This will give us V+ and V- at Point 1 in terms of V+ and V- at Point 2, as illustrated, below.
First, V+ at Point 1 in terms of V+ at Point 2:
Next, V- at Point 1 in terms of V- at Point 2:
Repeat for the total Current at Port 1:
The matrix form of these last two equations is:
The above 2x2 matrix is in the form of an ABCD matrix (note that I2's direction is defined as exiting the network, not entering it).
Two-Port Network Equations for Lossless Lines:
Sometimes it is convenient to assume a transmission line is lossless. What do I mean by lossless?
Recall the equation for the Propagation Constant: γ = α + jβ. If the line is lossless, α = 0 and thus e-γl becomes e-jβl.
The sinh term is similar: sinh(γl) = sinh(jβl) = -j*sin(j*jβl) = -j*sin(-βl) = j*sin(βl).
Resources:
For further reading...
"Some Broad-band Transformers", C.L. Ruthroff, Proceedings of the IRE,
August, 1959
"New Method of Impedance Matching in Radio-Frequency Circuits", G.
Guanella, The Brown Boveri Review, September, 1944
"Transmission Line Transformers," Chapter Six of Radio Frequency Circuit
Design, W. Alan Davis, Krishna Agarwal, John Wiley & Sonse, Inc. 2001
"A novel topology of Broad-band Coaxial impedance transformer", Centurelli,
Piatella, Tommasino, Trifiletti, Proceedings of the 40th European Microwave
Conference"
Phasors and Transmission Lines
And viewing...
Transmission Line YouTube Series,
Professor Gregory D. Durgin, Georgia Tech. Starting with this
video: https://www.youtube.com/watch?v=7Oz1sazpekM
Standard Caveat:
As always, I might have made a mistake in my equations, assumptions,
drawings, or interpretations. If you see anything you believe to be in
error or if anything is confusing, please feel free to contact me or comment
below.
And so I should add -- this information is distributed in the hope that it
will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty
of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE.




































No comments:
Post a Comment