Now I'm going to build one.
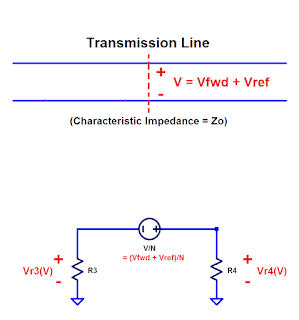
I'm using the Tandem Coupler topology (see previous post). Here's what the circuit will look like:
Why 16 turns?
I want enough turns on the transformer to present a high impedance on 160 meters, but not so many turns that they effect performance on 6 meters. So, I want to minimize the number of turns used and try to find a core with a high mu. But too few turns also means that the terminations on the FWD and REF ports will need to dissipate higher power.
With this in mind, my goal for the Coupling-factor (coupling of Input port to Forward port) is -24 dB, which means 16 turns on a transformer whose primary is a single turn (i.e. 20log(16) = 24).
Note that if the coupling from IN port to FWD port is -24 dB, then the power at the FWD port will be P(in) * 0.004 (i.e 24 dB down). So if power at the IN port is 100 watts, there will be 0.4 watts at the FWD port (important because the 50 ohm load on this port must be able to dissipate this power).
But what cores to use? Let's go to the junkbox and see what I can dig up...
Here are some I dug up. I believe these are primarily used for RFI mitigation applications, but they are made of type-43 material. Let's see if they'll work.
Note that they are ferrite, not powdered-iron (link to datasheet is at the end of this post). Per N8LP's QEX article (see link at end), ferrite cores are more prone to saturation than are powdered-iron cores. I don't know how much power these cores will tolerate -- I'll have to experiment. [Update: more info on applying these cores here: http://k6jca.blogspot.com/2015/07/antenna-auto-tuner-design-part-5.html and here: http://k6jca.blogspot.com/2015/12/antenna-auto-tuner-design-part-8-build.html]
I'll need sufficient inductance at 1.8 MHz to ensure that the voltage-sense transformer presents a high impedance compared to 50 ohms. I wound test coils on two of these cores, each with 16 turns of wire, and then I measured their inductance (these are not the coils I'm actually building the coupler with). They were 1.1mH and 0.7mH, respectively (measured on GenRad 1657 Digibridge, at 1 KHz). I don't know why there's a difference in inductance, but I suspect it's due to a variation in the ferrite core mu.
Another important Directional Coupler parameter is Directivity. Here, Directivity is defined as the coupling from the OUT-to-REF ports minus the coupling from IN-to-REF ports. Directivity affects SWR accuracy -- poor directivity means that "forward" power is getting into the "reflected" power port and corrupting the reading. So my goal is to have Directivity be at least -40 dB over the HF range (1-30 MHz, and ideally up to 54 MHz, but I'm also willing to sacrifice a bit at 6 meters if it gets me better performance at 30 MHz and below).
Some notes on construction:
1. For the "one turn" winding I ran a straight piece of Thermax MIL-C-17 spec RGU-142 coax through each transformer.
- The Max Power specification of this coax is 2,400 watts at 100 MHz. Not bad!
- This coax's max working voltage is 1400 V (not sure if that's a peak V or an RMS spec). Note that for an SWR of 1:1, 100 watts Forward Power into 50 ohms equals 100V peak, on the transmission line (if the SWR were infinite and Forward Power were still 100 watts, this peak voltage becomes 200V). And at 2000 watts and 1:1 SWR, Peak V is 442 volts. So at an infinite SWR peak voltage for 2000 watts of forward power would be 884 V, peak.
3. I used insulated wire in lieu of enameled wire for the transformer secondary windings. Insulation breakdown is especially important for the voltage-sense transformer, whose 16-turn secondary is across the coax. So, if SWR were infinite and Forward Power were 100 watts, there will be 200V, peak, across the windings of this transformer.
4. In the box I added a center-divider (made of PCB stock) between the two transformers. I found through experimentation that this divider should fully contact the three sides of the case in which I was mounting it. This was a problem because my case is aluminum; I can't solder to it. So I lined the inside of the case with copper tape and soldered the divider to it. Note: all tape seams were soldered along their entire length.
Here's the result. For my first tests, I'm going to call the lower-left port the IN port, the upper-left port is the OUT port (but this will later change, as you will discover further on...)
In the above image, the FWD port (relative to the IN port) is the lower-right port, and the REF port is the upper-right port.
Measuring and Improving Performance:
Let's make some measurements with a Vector Network Analyzer (VNA). Here's my test setup with an HP 3577A and matching S-parameter unit.
Directivity will be all important, so I want to see what I can do to minimize the coupling between the IN port and the REF port (because the coupling from OUT-to-REF is fixed at -24 dB).
Before I start experimenting, let's get a baseline. Here's a plot of Coupling, IN port to REF port, 0.1 - 100 MHz:
Directivity is the coupling shown above reduced by the forward coupling (-24 dB for 16 turns), so it will be 24 dB worse than the image above.
Can I improve Directivity? Time to experiment (this is where the design becomes more art than science). Here are some examples of what I tried...
If I move this wire closer to the case (using an insulated stick)...
There's an improvement. The coupling is lower by about 5 dB at 30 MHz, for example.
So I incorporate this "gimmick" of wire routing. Now, let's put cover on. Here's the cover, screwed down.
Note that the response has worsened.
But, if I remove just one screw...
...there's an improvement!
Yikes!
This is why there's an art to RF -- it's difficult to simulate these types of effects.
Another example of stray and parasitic effects...as I move a copper plate over the top, touching one side of the case but not both sides of the case...
...performance improves!
But if I continue to move the copper across the case until it's also touching the opposite side (straddling the case)...
...performance worsens by 10 dB at 54 MHz!
Long story short...after spending much time trying to improve performance when the case was screwed on, I finally decided that I wasn't really advancing. So, it was time to move on to the next step: characterizing the coupler's performance.
But, while making these characterization measurements I discovered that the ports are not quite symmetric in their performance. Specifically, there's a difference in Directivity, depending upon which port we define to be our "IN" port.
With this new data, I redefined the port configuration to maximize Directivity performance from 1 to 30 MHz. Here are the new port assignments:
And here's the Directional Coupler's characterization data for this new configuration.:
(click on image to enlarge)
Note that I've assigned the ports so that the Directivity data with the yellow background is appreciably better than the "Reverse Directivity." This is because, in my applications, I will be applying power to the IN port, and thus I want to minimize any coupling of this power to the REF port.
(I don't know why there is a difference in directivity. But if I want that additional performance at 54 MHz (about 2.5 dB improvement in Directivity), all I need to do is swap the In and Out connections and swap the FWD and REF connections).
Here's a drawing showing the construction connections in better detail:
(click on image to enlarge)
(Note the "gimmick" of routing one of the wires closer to the wall of the case.)
And some additional pictures...
Voltage-sense transformer on left (connected between REF (top) and FWD (bottom) ports):
Current-sense transformer on right (connected between OUT (top) and IN (bottom) ports):
Plots of the four coupling parameters (1 - 100 MHz)
(click on images to enlarge)
IN-port to FWD-port:
OUT-port to REF-port:
IN-port to REF-port and OUT-port to FWD-port:
Although they ought to be identical (or close to it), this image shows that the IN-port to REF-port coupling is noticeably different from the OUT-port to FWD-port coupling. Note the difference at 30 MHz and below. The IN-port to REF-port coupling is significantly lower (what we want!).
A plot showing actual Directivity (I'm measuring IN-to-REF, but after first normalizing the measurement of OUT-to-REF to 0 dB. That normalization factor is then automatically applied to this new measurement).
For the sake of completeness, here is what the OUT-to-FWD coupling looks like over the range of 0.1 - 200 MHz (the full range of the 3577A Network Analyzer). (Note that the IN-to-REF plot is about the same). Horizontal divisions are 20 MHz. Note that the hump just to the right of the middle of the plot is right around 144 MHz. Therefore expect very poor performance (because of poor directivity) on 2 meters!
Here's an interesting photo. This is what happens to the IN-port to REF-port coupling when the coupler's top cover is removed...
Here's the coupler, case screwed on.
Other Measurements
(Note that these were made before I reassigned the ports. Never the less, they should be close to the values of the reassigned ports).
Let's take a look at S11 in the IN port with all other ports terminated in 50 ohms. Here's the setup:
First, for reference, look at just S11 of the 50 ohm reference that I will attach to the coupler's "output" port (roughly -65 dB at 54 MHz).
And here's S11 of the terminated coupler. Roughly -27 dB (apologies for the blurriness) at 54 MHz.
S11 of same configuration on Smith Chart:
S11 with all ports unterminated. That is, S11 of just the coupler itself.
Measuring Self-Resonant-Frequency (SRF) of the 16-turn coil. Coil is paralleled with 50 ohm load, thus no cables, to minimize the effect of cable capacitance on SRF. Look for dip in S11.
S11 plot. And a nice dip at 10 MHz. That's the SRF (I don't know why there is a second dip).
Hmmm...I wonder if performance would improve if the SRF were higher...
Directivity and SWR Uncertainty:
Directivity has a direct effect upon VSWR error -- the poorer Directivity is, the more uncertain will be the VSWR reading (that is, the more uncertain will be the measured Return-Loss).
For example, if Directivity is -40 dB, VSWR uncertainty is fairly small for VSWRs under, say, 5, as shown in the graph below. That is, if your VSWR measures 5:1 or better, the actual SWR will be close to that value.
Let's say the measured SWR is 3:1. If our directivity is -40 dB, then the SWR might actually be somewhere between 2.9:1 and 3.1:1 -- in other words, VSWR will be within a narrow range that's essentially equal to 3:1.
But as Directivity worsens, uncertainty grows. If Directivity = -30 dB, then a measured VSWR of 3:1 could, in reality, be a VSWR anywhere between 2.7:1 and 3.4:1.
Or let's say Directivity is only -20 dB. Now, if we measure a VSWR of 3:1, the actual VSWR could be anywhere from 2.3:1 to 4.6:1. And this spread widens significantly for VSWRs greater than 3:1, as seen in the graph below.
And for reference, here's the graph for -35dB Directivity (my Coupler at 54 MHz):
Note: These graphs were each calculated using an EXCEL calculator, "VSWR Uncertainty versus Directivity, Return-Loss", which can be downloaded via a link in the "Links" section, below. I'm assuming the equations in the spreadsheet are correct.
Other Notes and Comments:
- Ground only one side of each coax cable that runs through the cores, not both sides!
- Experiment with which ends of the transformer windings connect to ground and which ends connect to ports. For example, the Voltage-sense transformer could connect to either the IN port or the OUT port, and also either end of the 16 turns of this transformer could go to this selected port. These choices do affect performance. You will need to experiment and discover which connections give the best response.
- Experiment with grounding one side or the other of the shields of each of the "one turn" coax cables.
- A Network Analyzer has been invaluable. I don't know how I would have tested this coupler without one.
- And many thanks to Dick Benson, W1QG, for his invaluable help and advice!!!
>>> Important Updates!!! <<<
For additional information on designing Direction Couplers, please see this later post: http://k6jca.blogspot.com/2015/07/antenna-auto-tuner-design-part-5.html .
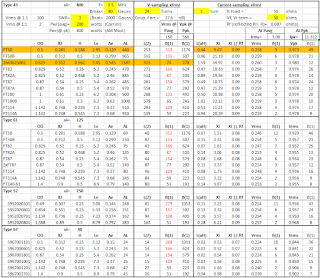
As part of the Directional Coupler design in this post I analyze core selection (among other things). Serendipitously, my core choice (above), Fair-Rite 2643625002, looks pretty good, per my spreadsheet below (see http://k6jca.blogspot.com/2015/07/antenna-auto-tuner-design-part-5.html for more details).
(click on image to enlarge)
Links to my Directional Coupler blog posts:
Notes on the Bruene Coupler, Part 2
Notes on the Bruene Coupler, Part 1
Notes on HF Directional Couplers (Tandem Match)
Building an HF Directional Coupler
Notes on the Bird Wattmeter
Notes on the Monimatch
Notes on the Twin-lead "Twin-Lamp" SWR Indicator
Calculating Flux Density in Tandem-Match Transformers
And some related links from my Auto-Tuner and my HF PA posts:
Auto Tuner, Part 5: Directional Coupler Design
Auto Tuner, Part 6: Notes on Match Detection
Auto Tuner, Part 8: The Build, Phase 2 (Integration of Match Detection)
HF PA, Part 5: T/R Switching and Output Directional Coupler
Useful Links:
Directivity and VSWR Measurements
Bird, Straight Talk about Directivity
Mini-circuits, Table, Return Loss vs VSWR
EXCEL Calculator, VSWR Uncertainty versus Directivity, Return-Loss
Fair-rite 2643625002 datasheet
Thermax RGU-142 Coax Datasheet
Philips, Design of HF Wideband Power Transformers, Part 1
Philips, Design of HF Wideband Power Transformers, Part 2
N8LP Wattmeter (QEX Article)
N2PK Power and Return-Loss Meter
And Finally, the Standard Caveat:
I could have easily made a mistake in any of the above, so please approach this material with a bit of skepticism -- don't assume it's correct. And if you do find an error, or would like more detail, please feel free to contact me.
Notes on the Bird Wattmeter
Notes on the Monimatch
Notes on the Twin-lead "Twin-Lamp" SWR Indicator
Calculating Flux Density in Tandem-Match Transformers
And some related links from my Auto-Tuner and my HF PA posts:
Auto Tuner, Part 5: Directional Coupler Design
Auto Tuner, Part 6: Notes on Match Detection
Auto Tuner, Part 8: The Build, Phase 2 (Integration of Match Detection)
HF PA, Part 5: T/R Switching and Output Directional Coupler
Useful Links:
Directivity and VSWR Measurements
Bird, Straight Talk about Directivity
Mini-circuits, Table, Return Loss vs VSWR
EXCEL Calculator, VSWR Uncertainty versus Directivity, Return-Loss
Fair-rite 2643625002 datasheet
Thermax RGU-142 Coax Datasheet
Philips, Design of HF Wideband Power Transformers, Part 1
Philips, Design of HF Wideband Power Transformers, Part 2
N8LP Wattmeter (QEX Article)
N2PK Power and Return-Loss Meter
And Finally, the Standard Caveat:
I could have easily made a mistake in any of the above, so please approach this material with a bit of skepticism -- don't assume it's correct. And if you do find an error, or would like more detail, please feel free to contact me.