I will:
- Select the values of inductors
- Calculate the maximum RMS voltage across each inductor
- Determine if an inductor should be air-wound or wound on a toroidal core
- Investigate which type of toroid core to use
- Calculate power dissipation due to iron powder toroidal core loss
- Estimate coil wire lengths for both air-wound and toroidal-wound inductors
- Calculate wire resistance and the resulting power dissipation of different gauge wires, per wire length for each coil.
Selecting the Inductor Values
Again, I'm going to assume that the worse-case SWR that I want to match is 10:1, and that the maximum power is 200 watts (average) and 800 watts, peak.
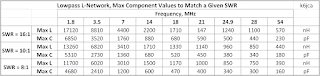
Here's the table I created of the maximum L and C values required to match any load with an SWR of 10:1:
(click on image to enlarge)
As you can see, at 3.5 MHz I should have at least 6820 nH of inductance to guarantee a match anywhere on the Smith Chart's 10:1 Constant SWR Circle.
And I'd like to have the smallest inductor be less than the 50 nH used by Elecraft in their KAT500 -- at 30 and 54 MHz it is this inductance, and not their smallest capacitance, that is the limiting factor in fine-tuning SWR (see http://k6jca.blogspot.com/search/label/Elecraft%20KAT500
So let's say that I simply halve this value to 25 nH and call it my smallest inductor.
If I do this, then, stepping inductor values in powers of 2, the resulting inductors would be
25 nH
50 nH
100 nH
200 nH
400 nH
800 nH
1600 nH
3200 nH
These sum to 6375 nH -- not quite my coal of 6820 nH, but close. Is it close enough?
I ran a quick simulation with a Matlab routine I wrote -- I'd still be able to tune any 10:1 SWR down to 1.2:1 or better (usually better) with 6375 nH as the max inductance. So, as a first cut, these values are close enough.
If I were very very picky, I could make the smallest inductor, say, 27.5 nH. This would result in values of 27.5, 55, 110, 220, 440, 880, 1760, and 3520 nH, for a total inductance of 7012 nH. More than enough.
But, to be honest, I like the simplicity of the first set of values (25 nH - 3200 nH) and for the moment I'm going to go with them. But -- I might decide to change my mind later.
To summarize: My initial selections of inductor values are these:
25 nH
50 nH
100 nH
200 nH
400 nH
800 nH
1600 nH
3200 nH
With these values of inductance and the values of capacitance selected in my previous post (see the values listed in the summary at the end of that post, here), what would this tuner's "Match Space" look like?
Here's the "Match Space" at 3.5 MHz:
(click on image to enlarge)
Not too bad! Just slightly inside the 10:1 SWR circle for reflection coefficients with angles between about -45 and 45 degrees.
And here it is at the other end of the spectrum, 30 MHz:
(click on image to enlarge)
Looks good. I believe this will work.
And although I don't plan to operate on 160 or 6 meters, here's how the match space looks on those two bands:
(click on image to enlarge)
Yes, not too great on 160 meters. Really needs more L and C.
(click on image to enlarge)
6 meters is probably tunable. But if I were serious about using the tuner on this band I would probably make both the minimum capacitance and the minimum inductance values smaller.
OK, so the match-space looks about what I'd expect it to be. Let's continue on...
One question I need to answer:
Which coils will be Air-Wound and which will be on an Iron-Powder Core?
To minimize coil loss, I'd like to "air wind" (air core) as many inductors as possible, but there will be size constraints and coupling constraints (inductor-to-inductor, inductor-to-other-stuff) that will limit which inductors should be air-wound solenoid coils and which should be wound on iron powder toroid cores.
As a starting point (which will probably change), I'm going to say that:
- The 25, 50, 100, 200, and 400 nH inductors will be air wound.
- The 1600 and 3200 nH inductors will be wound on iron powder toroid cores.
- And the 800 nH inductor might be air wound (preferable), or it might be on a toroid core.
Calculating Maximum Coil Vrms
I'm using maximum Vrms (based on a 200 watt average) instead of Vpeak (based on 800 watts, peak) because the end result of the following calculations will be coil power dissipation. And thus, because this heating of an inductor does not occur immediately, but rather over time, the RMS voltage value is more appropriate to use.
The inductors are connected in series, and I've calculated (using Excel) the max Vrms across the total inductance as the load reflection-coefficient is stepped around a Smith Chart's 10:1 SWR Circle. I can then easily sort this data for the maximum voltage value.
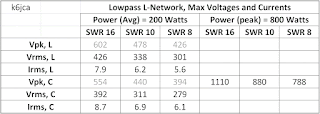
And for a power in of 200 watts and at an SWR of 10:1, the max Vrms voltage across the entire inductance is 338 V.
The table below summarizes these calculations. Note that they are independent of frequency.
(click on image to enlarge)
But to use the "Mini Ring Core Calculator", I need to know the voltage across each inductor, rather than the voltage across the entire inductance. Luckily, this isn't too hard to calculate (especially with Excel and Matlab available). Using the previous data generated via Excel, I wrote a simple Matlab routine that calculates voltage across each inductor as the load's reflection coefficient is moved around a Smith Chart's 10:1 SWR Circle (with Power In = 200 Watts).
Here's a graph showing how these voltages change at 3.5 MHz.
(click on image to enlarge)
And here's a similar graph showing the voltage changes at 30 MHz.
(click on image to enlarge)
The maximums of the inductor voltages shown in these charts (and those for the other bands of interest) are collected in the table below:
(click on image to enlarge)
So let's plug these values into "Mini Ring Core Calculator" and start figuring out what these inductors should be!
I'll start with the 3200 nH inductor. It's only used on 3.5 and 7 MHz, per the above table. And let's look at the programs results for this coil at 3.5 MHz (max Vrms = 300 V). I've assumed that the toroidal core is a T157-6 core.
(click on image to enlarge)
Note the two numbers in red at the lower right. One is "Flux" (actually, Flux Density), and the other is "Temperature Rise". Of these two numbers, it is the Temperature Rise value that is the important number (Flux Density really just feeds into the Temperature Rise Calculation).
Why is Temperature Rise important, and what should it be limited to?
At the end of the post I've linked to a number of Amidon and Micrometals data sheets and app notes. Here's a summary of the data regarding flux density and temperature:
- Iron Powder materials can tolerate up to 5000 Gauss without significant saturation effects (Amidon).
- Overheating of a core will take place long before saturation (in most applications) (Amidon).
- Flux Density Limits (i.e. the "max. Flux" box in the screen capture above) is used as a guideline to avoid excessive heating (Amidon).
- All iron powder cores are susceptible to permanent increases in core loss when exposed to elevated temperatures for extended periods of time. This thermal aging is irreversible. (Micrometals).
- If a core is used intermittently, keep its operating temperature below 100° C (Amidon).
- If a core is used continuously, keep its operating temperature below 75° C (Amidon).
- Long term operation of iron powder cores above 80° C can cause a permanent reduction in both Q and inductance. (With constant power dissipation, it typically takes a core about 2 hours to reach its final temperature) (Micrometals).
The Mini Ring Core Calculator's "Temperature Rise" value turns red for delta-T's of 50° C or more. So a good design target is to design an inductor so that its temperature rise is less than 50° C.
(Note -- a delta-T of 50° C over an ambient of 25° C results in a core temperature of 75° C, which isn't bad. But if the circuit is inside a box that has little or no internal airflow, the box's internal ambient temperature will be higher. If, say, the box's internal ambient is 50° C, then core temperature could be 100° C, and this would concern me.)
Below are tables with the Calculator's results for 3200, 1600, and 800 nH inductors (using the max voltages when power-in is 200 watts and SWR is 10:1), with different core sizes and materials.
Here's the table for the 3200 nH inductor. The values in red reflect the red values returned by the Calculator:
(click on image to enlarge)
Although the T157-6 core is probably acceptable, I prefer to be conservative in this design and so I lean towards the last three (T184-6, T157-17, or T184-17). The T157-17 and T184-17 cores both have very good core-loss numbers. Of these two, I'm going to choose the last one: 19 turns on a T184-17 core.
Here's the comparison table for the 1600 nH inductor:
(click on image to enlarge)
Of these four, I only really like the last two (again, core loss looks pretty good). Both use type-17 material. Of these two, I'm going to choose the last one: 14 turns on a T184-17 core.
And finally, here's the comparison table for the 800 nH inductor:
(click on image to enlarge)
None of these look great. Even the type-17 material in the T184 core becomes excessively lossy, in my opinion. So I'll try to make this coil air-wound.
So to summarize, the inductors wound on toroid cores, thus far, are:
- 3200 nH: T184-17, 19 turns. Wire diameter to-be-determined.
- 1600 nH: T184-17, 14 turns. Wire diameter to-be determined.
A couple of quick note on '6' versus '17' material. As you can see from the tables above, the '17' material has better loss characteristics. It's only drawback (as far as I can tell) is a slightly worse temperature coefficient, but I don't think this difference is too significant. Below are Amidon's TC charts. The first contains the curve for -6 material, the second contains the curve for -17 material.
Also, per Amidon pricing, the 17 material is more expensive than the 6 material. Not a big deal for a "one off" design like this, but something to be aware of if one were designing a product.
(click on image to enlarge)
(click on image to enlarge)
So if the core of an inductor built using type-17 material rises to 100° C, inductance will change by about 0.5%. That's acceptable, in my opinion.
Toroid Core Wire Diameter
What should the wire diameter be? As frequency increases skin-effect will become more pronounced and thus losses will increase, so the "thicker" the wire is, the better.
Using an on-line "AC Resistance" (i.e. skin-effect) calculator (here: http://chemandy.com/calculators/round-wire-ac-resistance-calculator.htm), I've calculated the AC resistance of different wire gauges at different frequencies:
(click on image to enlarge)
If I use these resistance numbers (in ohms-per-inch) and multiply them by the wire length determined by the Mini Ring Core Calculator program, I can determine power loss due to resistance.
So...for each toroid coil, I've taken its highest frequency of operation (where we should see the highest loss due to skin effect) and assumed the worst current (6.2Arms). The different wire lengths for a particular coil in the tables below represent the different amounts of wire required for the various core options (size and number of turns -- see the inductor tables, above).
The resulting power loss, versus wire gauge, is:
(click on image to enlarge)
(Note that, although the table above shows the 800 nH coil as being wound on a toroid core, I'm going to try to make it an air-wound solenoid coil, instead).
To minimize wire loss, I'd like to use 12 AWG, if possible (and I have a roll of it). (And I'll give 10 AWG a try, too, but if these gauges are too unwieldy to use, I might need to fall back to 14 AWG).
Total toroid coil loss will be the sum of two losses: core-loss plus wire-loss.
OK, let's move on to the air-wound inductors...
Air-wound Inductors:
I would like these inductors to be air-wound solenoid coils:
- 25 nH
- 50 nH
- 100 nH
- 200 nH
- 400 nH
- 800 nH
So, to use this calculator, I will first roughly estimate coil diameter and length. From these dimensions and the target inductance, the calculator returns:
- Number of Turns
- Wire Length
- Max AWG
When I'm satisfied with the results, I can take the calculated wire lengths and estimate total coil resistance (due to skin effect) for frequencies of interest.
Because I know the maximum RMS voltage across a coil (see earlier table), I can calculate the current passing through a coil (I = V/(2πfL)). With this current and the ESR I can then calculate the coil's loss (ESR*I^2).
I've run these calculations and I've put the results into the table below. Note that, in addition to power loss at 30 MHz, I've also calculated power loss at 54 MHz.
Note, too, that the 800 nH coil is calculated at 24.9 MHz (the highest frequency it's used for matching a 10:1 SWR), but I used the skin-effect resistance (ohms per foot) for 30 MHz.
(click on image to enlarge)
And finally, please note that these coil dimensions are really just place-holders to get an approximation of the wire lengths. These dimensions will probably change when I actually build the coils.
OK, that completes this preliminary inductor selection and design. Let's summarize...
Summary of Inductors:
(click on image to enlarge)
And a quick comment on these inductor values...they will change.
The relays and the interconnecting wires (or PCB traces) each have their own inductances (parasitic). To maintain my goal of a 25 nH step between successive inductance steps, I need to account for these parasitic inductances, otherwise I will have varying inductance deltas as I successively step through the values.
Conceptually, compensating for these parasitic inductances isn't hard to do, as I've described in the drawing below (showing the smallest three inductors, but the principle is applicable to all):
(click on image to enlarge)
If you go through the arithmetic you'll see that, with these new inductor values, the inductance delta is always 25 nH. As I said...conceptually easy. The "interesting" task will be determining what these actual parasitic inductance values are!
That's the end of this post! The next post will discuss relays and other components in the RF path.
The previous post, Part 2 -- Capacitor Selection, is here: http://k6jca.blogspot.com/2015/06/antenna-auto-tuner-design-part-2.html
Links to my blog posts in this Auto-tuner series:
Part 1: Preliminary Specification
Part 2: Network Capacitor Selection
Part 3: Network Inductor Selection
Part 4: Relays and L-Network Schematic (Preliminary)
Part 5: Directional Coupler Design
Part 6: Notes on Match Detection
Part 7: The Build, Phase 1
Part 8: The Build, Phase 2 (Integration of Match Detection)
Part 9: The Build, Phase 3 (Incorporating a Microcontroller)
Part 10: The Final Schematics
Resources:
Website, Amidon: http://www.amidoncorp.com/
Website, Micrometals:http://www.micrometals.com/
Data, Iron Powder Cores, Amidon: http://www.amidoncorp.com/product_images/specifications/1-02.pdf
Data, Iron Powder Materials, Amidon: http://www.amidoncorp.com/product_images/specifications/1-03.pdf
Data, Property Chart, Iron Powder, Amidon: http://www.amidoncorp.com/product_images/specifications/1-41.pdf
Data, Toroid Cores, Material 6, Amidon: http://www.amidoncorp.com/product_images/specifications/1-06.pdf
Data, Toroid Cores, Material 17, Amidon: http://www.amidoncorp.com/product_images/specifications/1-07.pdf
Data, Temperature Coefficients, Iron Powder Toroidal Cores, Amidon: http://www.amidoncorp.com/product_images/specifications/1-08.pdf
Data, Iron Powder Details, Micrometals: http://www.micrometals.com/materials_index.html
Data, Iron Powder Cores, General Properties, Micrometals: http://www.micrometals.com/materials_index.html
Data, Magnetic Tolerance versus Iron Powder Material, Micrometals: http://www.micrometals.com/materials_index.html
Data, Wire Diameters, AWG: https://en.wikipedia.org/wiki/American_wire_gauge
App Notes, Index, Iron Powder Cores (see "RF Applications" section), Micrometals: http://www.micrometals.com/appnotes_index.html
App Note, Design, "Power Considerations (Iron Powder and Ferrite)," Amidon: http://www.amidoncorp.com/product_images/specifications/1-35.pdf
App Note, "Power Considerations (cont')", Amidon: http://www.amidoncorp.com/product_images/specifications/1-36.pdf
App Note, Thermal Aging (Important note!), Micrometals: http://www.micrometals.com/thermalaging_index.html
Software, Toroid Inductor Calculator (including loss), Mini Ring Core Calculator: http://www.electronicecircuits.com/electronic-software/mini-ring-core-calculator-program
Calculator, Web, AC Skin Resistance (round wires): http://chemandy.com/calculators/round-wire-ac-resistance-calculator.htm
My Other Tuner posts:
A quick tutorial on Smith Chart basics: http://k6jca.blogspot.com/2015/03/a-brief-tutorial-on-smith-charts.html
The L-network: http://k6jca.blogspot.com/2015/03/notes-on-antenna-tuners-l-network-and.html
A correction to the usual L-network design constraints: http://k6jca.blogspot.com/2015/04/revisiting-l-network-equations-and.html
A look at highpass T-Networks: http://k6jca.blogspot.com/2015/04/notes-on-antenna-tuners-t-network-part-1.html
More on the W8ZR EZ-Tuner: http://k6jca.blogspot.com/2015/05/notes-on-antenna-tuners-more-on-w8zr-ez.html (Note that this tuner is also discussed in the highpass T-Network post).
The Elecraft KAT-500: http://k6jca.blogspot.com/2015/05/notes-on-antenna-tuners-elecraft-kat500.html
The Nye-Viking MB-V-A and the Rohde Coupler : http://k6jca.blogspot.com/2015/05/notes-on-antenna-tuners-nye-viking-mb-v.html
Standard Caveat:
As always, I might have made a mistake in my equations, assumptions, drawings, or interpretations. If you see anything you believe to be in error or if anything is confusing, please feel free to contact me or comment below.
And so I should add -- this design and any associated information is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE.
































No comments:
Post a Comment