Notes on Antenna Tuners: the Elecraft KAT500

I recently saw the Elecraft KAT500 in a friend's shack and I was impressed by its small size and fast tuning.  With an eye towards purchasing one, I thought I'd look into it further using the MATLAB analysis tools that I've recently written (see  http://k6jca.blogspot.com/2015/05/notes-on-antenna-tuners-more-on-w8zr-ez.html).

(By the way, for a quick review of Smith Chart's, go here:  http://k6jca.blogspot.com/search/label/Smith%20Chart).

The Elecraft KAT500 is based upon a lowpass L-network topology (a topology I much prefer over, say, a T-network.  If interested why, see:  http://k6jca.blogspot.com/2015/04/notes-on-antenna-tuners-t-network-part-1.html and http://k6jca.blogspot.com/2015/03/notes-on-antenna-tuners-l-network-and.html).

The KAT500 uses relays to select discrete "power-of-two" component values, rather than using the typical roller-inductor/variable-capacitor combo one often sees used to achieve a match.  I was curious how this tuner would perform given its minimum step sizes between component values (compared to the "infinitely small" step sizes between values that one gets with roller-inductors and variable caps).

I found the component step sizes (as well as maximum component values) in a very nice review of the KAT500, written by AD5X:  http://www.ad5x.com/images/Presentations/KAT500Review.pdf

In this review the author shows a screenshot of the menu for manually selecting capacitance and inductance values.  From the values listed, the maximum capacitance in 2701 pF and the maximum inductance is 17370 nH .

To keep things simple, I'm going to run my simulations assuming a step-size of 8 pF and 50 nH.  But note: actual step sizes are "roughly" related to 8 pF and 50 nH -- there is some variation due to the fact that the component values are not always in steps that are related by exact powers of 2.  E.g.  the next step up from 50 nH is 110 nH, rather than 100 nH).

So, making the assumption that capacitance step-size and inductance step-size were ideal at 8 pf and 50 uH, I thought I'd take a look at what loads the KAT500 will match to a 1:1 SWR (note, though, that the Elecraft specification is for matching to be within an SWR range of 1:1 to 1.6 to 1, so, per the Elecraft specification, the range of impedances will be larger than I show below).

Also, note that for the Elecraft plots below, the gaps between dots represent the 8 pF and 50 nH step sizes.  I had used arbitrary step-sizes when plotting other tuners, but because the Elecraft tuner is  specifically designed to use discrete steps in component values (rather than being infinitely variable), I used the tuner's actual minimum step size to create these plots.

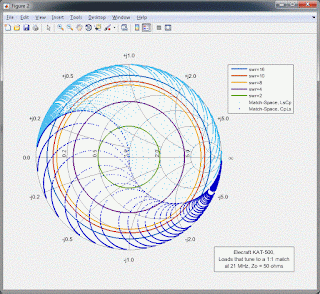
So let's look at the range of impedances it can match to an SWR of 1:1.  Here's the plot for 1.8 MHz.  Note that I show two "blue" areas.  One is for the tuner in its "LsCp" (series-L, parallel-C) configuration.  The other is for its CpLs configuration.

(click on image to enlarge)

 

The plot above represents the load impedances that can be tune to a 1:1 SWR, stepping through all combinations of component values.  Again, note that the Elecraft tuner is specified to tune to an SWR in the range of 1:1 to 1.6:1.  Relaxing the SWR limit to 1.6:1 will increase the area of the plot shown above.  For example, for a Zload = 9 + 0*j ohms (representing an SWR of about 5.6:1), the KAT500 should tune this impedance to an SWR that's about 1.6:1.

Note that at 1.8 MHz, Elecraft specifies that the KAT500 will tune to 1.6:1 or better for low-impedance loads whose SWR is limited to 5:1 and high-impedance loads whose SWR is limited to 10:1. I was curious what these low and high impedances actually were, so I ran another MATLAB routine to determine the reflection coefficients that meet these specifications.

(This other MATLAB routine assumes a PI network configuration, but by holding either the PI's Cin or Cout at 0 pF, I can simulate both the LsCp and CpLs L-network configurations.)

Here are two plots representing a march around the Smith Chart's 5:1 SWR circle in 5 degree increments at 1.8 MHz (again, assuming ideal component step-sizes of 8pF and 50 uH).  The first plot represents the LsCp L-network configuration, and the second plot is the CpLs configuration.

(click on images to enlarge)

As you can see, all loads along the "SWR = 5" circle (in 5 degree increments) can be matched to an SWR of 1.6:1, or better.

The range of "SWR = 10" reflection coefficients representing the impedances that can be matched to an SWR of 1.6:1, or better, lie along an arc on the Smith Chart's "SWR = 10" circle from about -95 degrees to +100 degrees (again, when measured in 5 degree increments), per the two plots below:

(click on images to enlarge)

 

Let's look at the range of impedances we can match to 1:1 at other frequencies.  Here's the range at 3.5 MHz:

(click on image to enlarge)

And here's 7.0 MHz.

(click on image to enlarge)

Very nice!  By the way, those "gaps" between arcs are related to the finite minimum inductance step size of 50 nH.

Here's the plot at 30 MHz.

(Click on image to enlarge)

Note that the gaps between the arcs have increased.

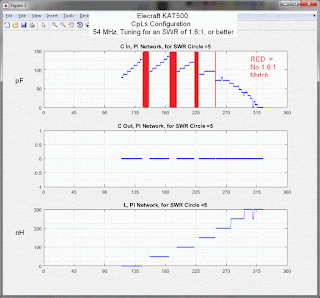
And here's a plot at 54 MHz (the KAT500 is spec'd to 60 MHz).

(click on image to enlarge)

 

As we can see from the plots above, as we increase frequency, the gaps between arcs become more pronounced.  Load impedances that fall within these gaps will not match to a 1:1 SWR, and, because the gap widths increase with frequency, this inability to match to 1:1 will be more pronounced on the higher bands.

Let's see what effect this has on the 6 meter band.  I'll pick a load impedance that's roughly midway between two of the "arcs" and that also has an SWR of 5:1:  10.65 + j12.21 ohms.

If I could set the tuner's components to L = 23.6 nH and C = 114.1 pF, we'd tune this load to an SWR of 1.02:1.  But I can't, because I'm limited to a step size of 8 pF and 50 nH.  Given these step sizes, the best SWR I can achieve for this load is about 1.8:1 (L = 50 nH, C = 88 pF). See the plot below:

(click on image to enlarge)

 

But this calculation was done assuming ideal components with infinite Q.  In reality, components will have "loss" -- the components are not infinite Q, and whatever power is dissipated by the components (via heating) is power that will not appear as reflected power and thus will lower the SWR.

Let's see what the matching range is given, say, capacitance Q of 2000 and inductance Q of 100 (I'm using these values because I don't know the actual KAT500 component Q's at 54 MHz).

If I use these values of Q in my other MATLAB routine and move around a Smith Chart's 5:1 SWR circle in 1 degree increments while attempting to tune the network to a 1.6:1, or better, SWR, I get the plot below when the KAT500 is in its CpLs configuration.  The red areas show where the program could not meet the 1.6:1 match specification.

(click on image to enlarge)

('C Out' is shown above, even though it is 0 (i.e. it doesn't exist), because the program is actually simulating a PI network.  I force either Cin or Cout to 0 pF to simulate either a LsCp or CpLs L-network).

On the other hand, the LsCp configuration looks fine, as we can see in  the plot below.  There are no areas where it can't tune to 1.6:1 for load impedances that have SWRs of 5:1. (The big gap is because the LsCp configuration is invalid in that region, and it is in this region that the CpLs configuration is used, per the plot above).

(click on image to enlarge)

Note that changing the length of the feedline slightly could help you achieve a match on 6 meters, should you find that your impedance lies in one of the "red bands" shown above -- a rotation of about 20 "Smith Chart" degrees (i.e. changing the feedline length by roughly a thirty-second of a wavelength, or about 4 inches on 6 meters, assuming a velocity factor of 0.6 ) should put you near a match sweet spot.

All in all, although there are some potential matching issues on 6 meters (related to minimum step size), the KAT500 looks like a very nice little tuner.

And I've just placed an order for one. 

By the way -- here's the part of my MATLAB script specific to the KAT500 calculations.  This code determines the load impedances that the KAT500 can match to 1:1:

(click on image to enlarge)

Essentially, this code connects 50 ohms to the INPUT of the tuner and then calculates the impedances seen looking into the tuner's OUTPUT terminals for all combinations of L and C.  These impedances are the complex-conjugates of the actual load impedances that the tuner can match to a 1:1 SWR.


More Notes on KAT500 Operation [Added 14 June 2015]

My KAT500 has arrived! And I thought I'd add a few more notes.

1.  A Note on Power Loss versus CpLs and LsCp L-Network configuration
While playing around with the KAT500, I wondered if there was a correlation between inductance value and power loss when using a Lowpass L-Network.  That is, did power loss increase as inductance increased (as we move around a Smith Chart's "Circle of Constant SWR" (and assuming inductance Q is significantly worse than capacitance Q)?

Well, not really, as you can see from the plot below...

(click on image to enlarge)

Max power loss occurs while inductance is increasing, rather than aligning with the inductance curves.  So power loss does not correlate well with inductance.

BUT, there is useful information here, never the less...

Given a Lowpass L-network, maximum power loss occurs in the CpLs configuration (inductance in series with load).

And if in the LsCp configuration (which usually has lower power loss than the CpLs configuration), power loss does correlate with inductance value.

So, if you can adjust the length of your feedline, my opinion is: try to adjust it so that...

1. The L-Network is in its LsCp configuration for as broad a frequency swath as possible (rather than the CpLs configuration), and
2. The value of L is minimized.

These two rules should minimize power loss due to current through the inductor's parasitic resistance.

If you cannot do both of these, then I would shoot for one or the other.  But it's difficult to say if you should minimize L in the CpLs configuration over choosing the LsCp configuration if the LsCp configuration has a higher value of L.  This decision really depends upon the Q of the components being used, and I don't know what the Q's are in the KAT500.

How can I specifically apply this knowledge to my KAT-500?

Elecraft has a nifty utility program that can be used with the KAT500 and which will show you the state of its configuration. I have the ability to change the length of my feedline in a couple of discrete steps (I added this ability so that my Icom AT-500 auto-tuner could tune my 80 meter loop), and I can use the KAT500 utility program to select the "optimal" feedline length (of the four lengths available to me).

Here's a screenshot of the tuner's configuration at the "default" feedline length -- no extra length of feedline added (frequency is 3.865 MHz):

(click on image to enlarge)

Here's the tuner configuration with an additional "Length 1" of feedline added:

(click on image to enlarge)

Here's the tuner configuration with and additional "Length 2" of feedline added:

(click on image to enlarge)

And finally, here's the tuner configuration with both lengths (1 and 2) of feedline added:

(click on image to enlarge)

If you look at these four configurations you should see:

1. Default feedline configuration:  CpLs configuration (caps are on the transmitter side of the network, not the antenna side).. L is 750 nH, but SWR only gets to 1.61 (and at 3.825 MHz the minimum SWR, when tuned, is 2.06).
2. Length 1 configuration: LsCp configuration (good) -- note that the "Caps on Ant Side" box is checked.  But inductance is 2330 nH -- the highest value of any of these 4 configurations.
3. Length 2 configuration:  CpLs configuration.  L is 2100 nH. And minimum SWR is 1.57 (And at 3.9 MHz the minimum SWR is 2.0 -- not great.)
4. Length 1 & 2 configuration:  CpLs configuration, but L is 480 nH.

Both the Default feedline configuration and the "Length 2" configuration have problems tuning below 2:1 at some frequencies (as noted above), so let's not use those.

The "Length 1" configuration is the desired "LsCp" network, but note from the graph at the introduction to this section:  in the LsCp configuration, power-loss directly correlates with inductance.  So, the higher the inductance is in the LsCp configuration, the worse will be the power loss when in this configuration.

The "Length 1 & 2" configuration has both a low inductance and a low SWR. But is the power-loss in this configuration better than the "Length 1" configuration?  It's difficult for me to say, because this really depends upon the parasitic resistance of the inductors.  But given that the inductance in the "Length 1 & 2" configuration is so low (480 nH, compared to 2330 nH), that's the feedline configuration I'm using.


2.  The Effect of Actual Component Values

The simulations above were performed assuming fixed C and L step sizes of 8 pF and 50 nH.  But the KAT500 doesn't actually maintain a constant step size (which you will quickly see if you look at the values shown in the screenshots of the utility program above).

So I decided to rerun my Matlab simulations using the actual component values listed by Elecraft in the screen shot, above.  Note that these plots assume no additional parasitic effects.

Here are the plots:

1.8 MHz

(click on image to enlarge)

 

3.5 MHz

(click on image to enlarge)

 

7 MHz

(click on image to enlarge)

 

14 MHz

(click on image to enlarge)

 

21 MHz

(click on image to enlarge)

 

30 MHz

(click on image to enlarge)

 

54 MHz

(click on image to enlarge)

 

The unevenness in the "gaps" in the plots are due to the non-constant L and C step sizes.  To get an idea of how these step sizes affect the "matching space," I've plotted out the first 17 steps of inductance (starting at 0 nH), with all the C steps for each value of inductance, on 21 MHz.  Note that, although the minimum L is 50 nH and the minimum C is 8 pF, the actual step size between successive values can be much larger (e.g. 90 nH and 29 pF).

(click on image to enlarge)

3.  A Small Problem Discovered...
[Added:  18 June 2015]

As I mentioned above, there were some frequencies on 80 meters that would not tune below a 2:1 SWR (depending upon the length of feedline selected).  I decided to take a closer look at what was going on, and I discovered a problem.

The problem is this:  in each instance in which the SWR auto-tuned to 2:1 (or worse), I was able to manually tune the KAT500 to a better SWR (usually under 1.4:1) using the KAT500 Utility program.

Well, this was a bit annoying -- if I could tune the tuner to a reasonable SWR, I'd assumed that the KAT500's algorithm would do the same, only faster.

I can't speak to why the algorithm doesn't do what, in my opinion, it should be doing.  But I can speak to what it is doing, and in my case it's this:

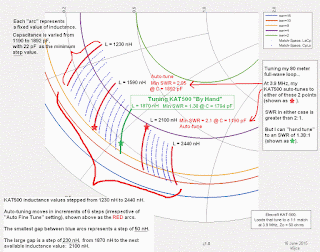
In the final tuning stage for this particular antenna and feedline length, at 3.90 MHz, the algorithm is stepping the inductance value in steps of six "inductance increments."  In doing so, it misses the tuning "sweet spot" and the step size is never reduced to search more closely for a better match.

Here's a drawing illustrating what I mean:

(click on image to enlarge)

In this particular example, rather than tuning to a single unique setting,  the KAT500 will auto-tune to one of two settings, both with an SWR of about 2:1.  I've represented these in the illustration with red "stars".

One of these settings has a capacitance of 1190 pF, and the other has a capacitance of 1892 pF.  So, in the plot above, for each step of inductance from 1230 nH to 2440 nH (which bracket the inductance(s) that the auto-tune selects for its best match), I've stepped the capacitance from 1190 to 1892 pF and plotted where on the Smith Chart the load would lie if the KAT500 were to match to a 1:1 SWR.  (In my case, the KAT500 isn't tuning to an SWR of 1:1, but the plot is useful for showing what is going on and what values are available for matching).

The red "arcs" represent the inductance values that the algorithm steps through in its final "fine tune" search.  As you can see, they are 6 steps apart.  (Capacitance is also rather coarsely tuned, too, but I haven't shown that -- instead I've simply shown every capacitance step available to the tuning algorithm between 1190 and 1892 pF).

The green star, lying on the green inductance arc, represents the sweet spot that I can manually tune the KAT500 to.

Clearly, to find this sweet spot, the KAT500 would need to reduce its step size.  But it doesn't, and to me this is a flaw in its tuning algorithm.

Fortunately, as I mentioned earlier, I can change the length of my feedline.  This lets me work around the flaw -- I can select a length that allows the KAT500 to achieve a good match all across the 80 meter band, without these 2:1 SWR tuning anomalies.  But if I were stuck with a fixed length of feedline (as most hams are) and I found this happening, I would be, well, more than a little annoyed.

[I'll add -- to Elecraft's credit, their team has been very responsive to my report of this problem. And for those who are interested, the firmware revision in my tuner is 1.67.]

Additional Note, 16 September 2015.  Some real-world measurements:

I'd just run some real-world match-space measurements on my own tuner design (here), and I was surprised by the results, which resulted in a modification to my design.  So I was very curious to see how the KAT500 compared.

To recap my earlier explanation (above), from Network Theory I know that if a network transforms an unknown impedance to 50 ohms, resistive, I can determine the value of that unknown impedance by terminating the network's "driven" port with 50 ohms (while keeping the network's values unchanged) and measuring the impedance at its "load" port.  The impedance I then measure should be the complex conjugate of the unknown impedance that had originally been connected to the network's "load" port.

So, to determine which loads the KAT500 will tune to a 1:1 SWR match, I just terminate the 'XMTR' side of the tuner with 50 ohms and step through the various values of the network components while measuring the impedance presented at the tuner's 'ANT' port with my 8753A Vector Network Analyzer (VNA).

For each change of the network component values, this impedance measurement is transferred from the VNA to a Matlab routine running on my computer, which in turn converts the measured impedance to its complex conjugate.  In other words, the Matlab routine calculates the actual load impedance that would be transformed by those specific tuner settings to 50 ohms for the transmitter.

Here's the KAT500 test setup.  The VNA drives the tuner's Antenna port (VNA's Reference Plane shown) and terminating the Xmtr port in 50 ohms.

Here's a screenshot of the Matlab program (it communicates with my HP 8753A network analyzer) and the Elecraft KAT500 Utility while testing was in progress.

Here's the actual measured match-space for my KAT500 (s/n 1707) at 30 MHz.  It is significantly different from the "theoretical" match-space I calculated earlier, above.  Notice the unevenness in coverage.

Gaps (or jumps) in match-space coverage can be caused by the following effects, for example:

1. Parasitic series inductance.
2. Parasitic shunt capacitance to ground.
3. Differences between "ideal" (schematic) component values and their actual (manufactured) values.

(For additional details on how parasitic elements (particularly parasitic series inductance) can affect a tuner's "match-space", please refer to the "Testing" section in this post:   http://k6jca.blogspot.com/2015/09/antenna-auto-tuner-design-part-7-build.html)

By the way, in the measurements above, the "no L and no C" SWR measures 1.57:1 in CpLs mode and 1.51:1 in LsCp mode.

Below are plots of the outline of the match-space on different bands.  Please note that the points shown are a subset of all possible match-space points.  For example, to keep my test-time reasonable, I might make the component-value step-size 0x04 in lieu of the minimum step size of 0x01.  Similarly, I might limit the maximum value to something less than 0xFF.  Notes within each plot will identify both maximum value and step size.

Here's the plot of the match-space outline at 21 MHz.  Note that I only step up to 0x18 for both L and C (max would be 0xFF) and that the step-size is 0x01 (the minimum possible step size).

While running my first attempt at Power Loss testing with a 5 ohm load, I was surprised to find that I could not tune the KAT500 below an SWR of about 1.9:1 on 21 MHz (as measured with my HP 8753A). 

Although this value of 1.9:1 would shift around a bit, depending upon which Power Loss Measurement technique I was attempting (see here), I wondered why I couldn't get a lower SWR, and so I plotted part of the KAT500's Match-Space in the area of a 5 ohm load:

You can see the problem -- there's a large gap between the edges of the LsCp and CpLs match space and the 5 ohm load falls right in the middle of this gap.

This particular gap between the LsCp and the CpLs match spaces implies the presence of parasitic series-inductance (e.g. from the PCB traces and board wiring, etc.).  I would like to note that  gaps between the LsCp and CpLs match spaces cannot be fixed by simply changing the Ls or Cp component values (at least, to my knowledge).  Simply changing the values of the Ls and Cp components will move you along the existing "arcs" shown above, or shift the arcs within a match-space, but they will not bridge the gap between the two match spaces, because, along these particular borders of the match-space, either Ls or Cp is already 0 and cannot get any smaller.  As I discovered with my own tuner design (here), I had to add series capacitance (Cs) to compensate for an even worse Smith Chart "9 o'clock" gap (caused by parasitic series-inductance) exhibited in the implementation of my tuner design.

Here's the match-space plot for 14 MHz.  Note that I'm now using a step-size of 0x02.  (If 0x01 were instead used, there would be an additional measurement result between each pair of points below.)

Match-space outline at 7 MHz (stepped with a minimum step size of 0x04).

And finally, match-space outline at 3.5 MHz:

Note the jumps in the CpLs space.  I strongly suspect these gaps are the real issue underlying my problems with tuning on 80 meters (see the section, "A Small Problem Discovered...", earlier in this post).

That's it for "real world" testing.  I didn't bother to test 1.8 MHz or 54 MHz because I don't operate on those bands.


[Update, 21 October 2015:  Testing, Tuner Power Loss, 10:1 SWR]

After several attempts to measure Tuner Power Loss, I settled upon the "Gp" measurement technique, as I describe in this post: http://k6jca.blogspot.com/2015/10/notes-on-measuring-antenna-tuner-power.html

Here are those result for both the KAT500 and, for comparison, my tuner:

Please note, too, that the "Tuner Loss" post associated with the link above contains additional KAT500 Power Loss measurements, using other techniques.


Antenna Tuner Blog Posts:

A quick tutorial on Smith Chart basics:
http://k6jca.blogspot.com/2015/03/a-brief-tutorial-on-smith-charts.html

Plotting Smith Chart Data in 3-D:
http://k6jca.blogspot.com/2018/09/plotting-3-d-smith-charts-with-matlab.html

he L-network:
http://k6jca.blogspot.com/2015/03/notes-on-antenna-tuners-l-network-and.html

A correction to the usual L-network design constraints:
http://k6jca.blogspot.com/2015/04/revisiting-l-network-equations-and.html

Calculating L-Network values when the components are lossy:
http://k6jca.blogspot.com/2018/09/l-networks-new-equations-for-better.html

A look at highpass T-Networks:
http://k6jca.blogspot.com/2015/04/notes-on-antenna-tuners-t-network-part-1.html

More on the W8ZR EZ-Tuner:
http://k6jca.blogspot.com/2015/05/notes-on-antenna-tuners-more-on-w8zr-ez.html  (Note that this tuner is also discussed in the highpass T-Network post).

The Elecraft KAT-500:
http://k6jca.blogspot.com/2015/05/notes-on-antenna-tuners-elecraft-kat500.html

The Nye Viking MB-V-A tuner and the Rohde Coupler:
http://k6jca.blogspot.com/2015/05/notes-on-antenna-tuners-nye-viking-mb-v.html

The Drake MN-4 Tuner:
http://k6jca.blogspot.com/2018/08/notes-on-antenna-tuners-drake-mn-4.html

Measuring a Tuner's "Match-Space":

http://k6jca.blogspot.com/2018/08/notes-on-antenna-tuners-determining.html

Measuring Tuner Power Loss:

http://k6jca.blogspot.com/2018/08/additional-notes-on-measuring-antenna.html

Standard Caveat:

I could easily have made a mistake in my MATLAB program or in my post above.  If anything looks wrong, or if you'd like clarification, please feel free to contact me!

And if you'd like me to apply this MATLAB script to other networks, again, please feel free to contact me.